



Siguiente: Solubilidad de DSP
Un nivel arriba: Problemas en teoría de
Anterior: DSP
1. Sea K un campo. Un polinomio
![$P(X)\in K[X]$](img1963.gif) es
es
- irreducible si rige la implicación
- mónico si su coeficiente principal es 1.
Un elemento 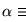 en una extensión de K es algebraico sobre K si existe un polinomio
en una extensión de K es algebraico sobre K si existe un polinomio
![$P(X)\in K[X]$](img1963.gif) tal que
tal que
 .
Si
.
Si 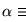 es algebraico existe un polinomio mínimo irreducible P(X) tal que
es algebraico existe un polinomio mínimo irreducible P(X) tal que
 ,
y es único salvo multiplicación por constantes. P(X), hecho mónico, es el irreducible de
,
y es único salvo multiplicación por constantes. P(X), hecho mónico, es el irreducible de 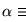 .
.
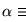 es entero algebraico si es algebraico y su polinomio irreducible es mónico con coeficientes enteros.
es entero algebraico si es algebraico y su polinomio irreducible es mónico con coeficientes enteros.
2. El conjunto de números algebraicos forma un campo.
3. El conjunto de enteros algebraicos forma un anillo.
4. Para todo algebraico 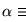 existe un entero racional m tal que
existe un entero racional m tal que 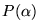 es un entero algebraico.
es un entero algebraico.
5. Si 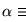 es algebraico y su irreducible es de orden n el conjunto
es algebraico y su irreducible es de orden n el conjunto
es una extensión de K de orden n.
Las extensiones de orden 2 se dicen ser cuadráticas.
6. Dados dos enteros algebraicos 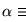 y
y 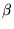 decimos que
decimos que 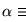 divide a
divide a 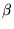 ,
,
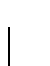 ,
si existe un entero algebraico
,
si existe un entero algebraico 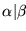 tal que
tal que
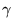 .
Los divisores de 1 se dicen ser unidades.
Las unidades forman un grupo multiplicativo.
.
Los divisores de 1 se dicen ser unidades.
Las unidades forman un grupo multiplicativo.
7. Si m es un entero racional que no es un cuadrado, entonces
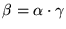 es un campo cuadrático. El conjunto de enteros algebraicos
es un campo cuadrático. El conjunto de enteros algebraicos
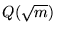 se caracteriza de la siguiente forma:
se caracteriza de la siguiente forma:
8. Un campo cuadrático real es de la forma
 donde
donde 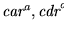 no es un cuadrado. Sus enteros son las raices en él de polinomios mónicos con coeficientes enteros.
no es un cuadrado. Sus enteros son las raices en él de polinomios mónicos con coeficientes enteros.




Siguiente: Solubilidad de DSP
Un nivel arriba: Problemas en teoría de
Anterior: DSP
Guillermo Morales-Luna
2000-07-10
![$P(X)\in K[X]$](img1963.gif) es
es
![$P(X)\in K[X]$](img1963.gif) tal que
tal que
 .
Si
.
Si  ,
y es único salvo multiplicación por constantes. P(X), hecho mónico, es el irreducible de
,
y es único salvo multiplicación por constantes. P(X), hecho mónico, es el irreducible de  ,
si existe un entero algebraico
,
si existe un entero algebraico  donde
donde