



Siguiente: Algunos otros problemas
Un nivel arriba: Problemas en teoría de
Anterior: Enteros algebraicos
Consideremos la versión de DSP consistente en decidir a validez de la fórmula
donde para cada 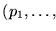
 son polinomios lineales con coeficientes enteros (racionales).
son polinomios lineales con coeficientes enteros (racionales).
1. En esta sección 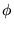 siempre denotará una fórmula de la forma
siempre denotará una fórmula de la forma
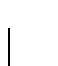 se dice ser positiva si puede expresarse de manera que todos los coeficientes que aparezcan en los polinomios son números naturales.
se dice ser positiva si puede expresarse de manera que todos los coeficientes que aparezcan en los polinomios son números naturales.
2. En lo sucesivo
 es una transformación afín.
Para una fórmula
es una transformación afín.
Para una fórmula
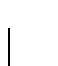 definimos
definimos
donde
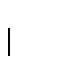 es una fórmula tal que se tenga
es una fórmula tal que se tenga
Escribiremos
 ,
y diremos que
,
y diremos que 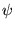 se obtiene de
se obtiene de 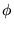 mediante el cambio de variable
mediante el cambio de variable
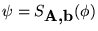 .
.
3. Un cono en Rn es un conjunto
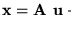 tal que
tal que
- Contiene al cero:
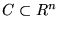 .
.
- Es cerrado bajo la suma:
- Contiene al semisegmento positivo de cada uno de sus elementos:
- No contiene parejas simétricas:
Por ejemplo, el primer ``2n-ante'' es un cono.
Si C es un cono la relación ``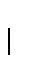 '' definida como
'' definida como
es una relación de orden.
Si C está definido por un predicado
diremos que
 define un orden.
define un orden.
4. Lema: Sea
donde
 define un orden,
define un orden,
 y
y
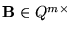 .
Entonces existe un conjunto de transformaciones afines
.
Entonces existe un conjunto de transformaciones afines
tal que
y
5. Lema: Dada una fórmula
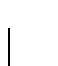 con coeficientes en Z se puede encontrar algorítmicamente un conjunto
con coeficientes en Z se puede encontrar algorítmicamente un conjunto
 de predicados que definen órdenes y un conjunto de transformaciones afines
de predicados que definen órdenes y un conjunto de transformaciones afines
tales que
y
6. Utilizaremos la notación siguiente
Lema: Si para algún exponente k y algún primo p tenemos que
y
entonces
7. Lema: Una fórmula de la forma
donde 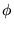 es positiva y
es positiva y 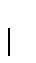 define un orden, tiene una solución en N si y sólo si
define un orden, tiene una solución en N si y sólo si
8. Teorema: Existe un algoritmo para decidir la veracidad de una fórmula
9. Corolario: DSP está en la clase NP.
10. Proposición: DSP es completo-NP
Veamos que el problema EDC de Ecuación Diofantina Cuadrática se reduce a DSP.
Dada una instancia
tenemos las siguientes relaciones
Consideremos entonces la instancia de DSP
Si 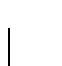 se resuelve, se prueba cada una de las posibles soluciones z, las cuáles forman un conjunto finito en la región determinada por el Teorema en la observación anterior y se ve si alguna es un cuadrado, en cuyo caso
se resuelve, se prueba cada una de las posibles soluciones z, las cuáles forman un conjunto finito en la región determinada por el Teorema en la observación anterior y se ve si alguna es un cuadrado, en cuyo caso 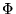 posee efectivamente una solución.
posee efectivamente una solución.




Siguiente: Algunos otros problemas
Un nivel arriba: Problemas en teoría de
Anterior: Enteros algebraicos
Guillermo Morales-Luna
2000-07-10
 son polinomios lineales con coeficientes enteros (racionales).
son polinomios lineales con coeficientes enteros (racionales).
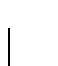 se dice ser positiva si puede expresarse de manera que todos los coeficientes que aparezcan en los polinomios son números naturales.
se dice ser positiva si puede expresarse de manera que todos los coeficientes que aparezcan en los polinomios son números naturales.
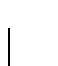 definimos
definimos
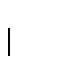 es una fórmula tal que se tenga
es una fórmula tal que se tenga
 ,
y diremos que
,
y diremos que  define un orden.
define un orden.
 define un orden,
define un orden,
 y
y
 con coeficientes en Z se puede encontrar algorítmicamente un conjunto
con coeficientes en Z se puede encontrar algorítmicamente un conjunto
 de predicados que definen órdenes y un conjunto de transformaciones afines
de predicados que definen órdenes y un conjunto de transformaciones afines
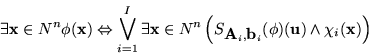
 se resuelve, se prueba cada una de las posibles soluciones z, las cuáles forman un conjunto finito en la región determinada por el Teorema en la observación anterior y se ve si alguna es un cuadrado, en cuyo caso
se resuelve, se prueba cada una de las posibles soluciones z, las cuáles forman un conjunto finito en la región determinada por el Teorema en la observación anterior y se ve si alguna es un cuadrado, en cuyo caso