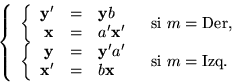Siguiente: Modelos restringidos de máquinas
Un nivel arriba: Máquinas de Turing
Anterior: Ejemplo: Cadenas equilibradas de
Computaciones en máquinas de Turing
Veamos aquí un enfoque formal a las máquinas de Turing.
Una máquina de Turing es una estructura de la forma
M=(Q,A,t,q0,F) donde,
De manera convencional se dice que
- M es determinista si t es una función
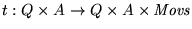 ,
,
- M es indeterminista si t es una mera relación,
Una descripción instantánea (DI) es una cadena de la forma
con
y-i=a0=xj c.t.p.-(i,j) (casi en todas partes resepcto a i,j). q es el estado de la DI. Su interpretación es, naturalmente, la siguiente:
``El contenido de la cinta es
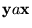 ,
se está examinando el carácter a y el control finito de la máquina está en el estado q.''
,
se está examinando el carácter a y el control finito de la máquina está en el estado q.''
Alternativamente podemos distinguir a un símbolo de marca `` '' para reconocer inicios y terminaciones de DI's.
Una DI es inicial o final según lo sea su estado. Si
'' para reconocer inicios y terminaciones de DI's.
Una DI es inicial o final según lo sea su estado. Si
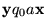 es inicial decimos que la descripción inicial corresponde a la entrada
es inicial decimos que la descripción inicial corresponde a la entrada
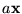 .
Si
.
Si
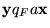 es final decimos que la máquina deja a la salida
es final decimos que la máquina deja a la salida
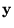 .
Escribimos
.
Escribimos
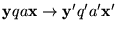 si es que existe una transición
si es que existe una transición
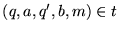 tal que
tal que
``
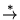 '' es la cerradura reflexivo-transitiva de la relación ``
'' es la cerradura reflexivo-transitiva de la relación ``
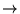 ''.
Si
''.
Si
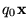 es inicial,
es inicial,
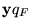 es final y
es final y
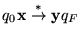 entonces decimos que M converge para la entrada
entonces decimos que M converge para la entrada
 y, escribimos
y, escribimos
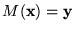 .
Si
.
Si
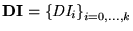 es una sucesión de DI's tal que
es una sucesión de DI's tal que
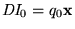 ,
,
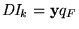 y
y
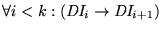 entonces decimos que
entonces decimos que
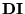 es una computación terminal que transforma la DI inicial en la final. Si
es una computación terminal que transforma la DI inicial en la final. Si
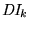 no corresponde a un estado final, la computación se dice ser intermedia.
Así pues, si M es una máquina y
no corresponde a un estado final, la computación se dice ser intermedia.
Así pues, si M es una máquina y
 es el contenido inicial en su cinta,
es el contenido inicial en su cinta,
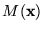 denotará al contenido que queda en la cinta cuando M se para a partir de
denotará al contenido que queda en la cinta cuando M se para a partir de
 .
Indicaremos que M no se para a partir de
.
Indicaremos que M no se para a partir de
 escribiendo
escribiendo
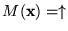 ,
en el cual caso, diremos que M diverge con
,
en el cual caso, diremos que M diverge con
 .
.




Siguiente: Modelos restringidos de máquinas
Un nivel arriba: Máquinas de Turing
Anterior: Ejemplo: Cadenas equilibradas de
Guillermo Morales-Luna
2000-07-10


, se está examinando el carácter a y el control finito de la máquina está en el estado q.''