



Siguiente: Computabilidad-Turing
Un nivel arriba: Máquinas de Turing
Anterior: Computaciones en máquinas de
Presentaremos algunas variantes de las máquinas de Turing y veremos que son equivalentes. Mostraremos las equivalencias entre las diversas modificaciones de las máquinas de Turing de manera más bien coloquial. Anque se puede presentar demostraciones rigurosas en base a descripciones instantáneas, aquí las omitiremos con la certeza de que el lector podrá construirlas a partir de las indicaciones que presentamos.
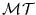 denotará a la clase de máquinas de Turing tal como las hemos definido.
Diremos que dos clases de máquinas
denotará a la clase de máquinas de Turing tal como las hemos definido.
Diremos que dos clases de máquinas
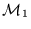 y
y
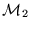 son equivalentes si toda máquina en una clase es simulada por una máquina en la otra, es decir,
son equivalentes si toda máquina en una clase es simulada por una máquina en la otra, es decir,
-
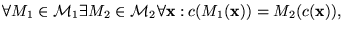 y
y
-
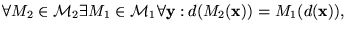
donde c y d son funciones apropiadas de conversión de palabras de un alfabeto a otro, considerando los alfabetos de ambas máquinas, que cumplen además
 .
Máquinas con cintas semi-infinitas,
.
Máquinas con cintas semi-infinitas,
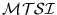 :
Estas son máquinas de Turing donde las casillas de la cinta se ponen en correspondencia con
:
Estas son máquinas de Turing donde las casillas de la cinta se ponen en correspondencia con 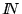 mas no con
mas no con 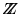 ,
es decir, la cinta de cada máquina de esta clase tiene una casilla inicial a la izquierda, digamos c0, y se prolonga indefinidamente a la derecha.
,
es decir, la cinta de cada máquina de esta clase tiene una casilla inicial a la izquierda, digamos c0, y se prolonga indefinidamente a la derecha.
Proposición 6.1
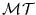
y
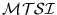
son equivalentes.
En efecto, por un lado, tenemos que toda máquina
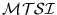 es en sí del tipo
es en sí del tipo 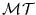 .
Recíprocamente, enumeremos las casillas de la cinta semi-infinita C como
.
Recíprocamente, enumeremos las casillas de la cinta semi-infinita C como
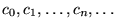 Dada una máquina M del tipo
Dada una máquina M del tipo 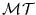 enumeremos a las casillas de la cinta de M como
enumeremos a las casillas de la cinta de M como
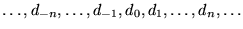 Pongamos un símbolo especial S en c0 e identifiquemos al sector ``negativo'' de la cinta de M con las casillas impares de C y al ``no-negativo'' de M con las casillas pares de C:
Pongamos un símbolo especial S en c0 e identifiquemos al sector ``negativo'' de la cinta de M con las casillas impares de C y al ``no-negativo'' de M con las casillas pares de C:
Observamos que el movimiento hacia una casilla contigua en la cinta de M se traduce a dos movimientos contiguos en C. Cada vez que se ``atraviesa'' S en C se cambia de sentido: Un movimiento a la derecha en M corresponde a dos hacia la izquierda en C y viceversa.
Hechas estas observaciones, de manera directa se puede simular a M usando C.
Máquinas con cintas de varias pistas,
 :
Estas son máquinas de Turing cuyas cintas tienen varias ``pistas''. Pueden verse también como máquinas de varias cintas con movimientos ``sincronizados'': Movimiento que se hace en una cinta, se hace en todas.
:
Estas son máquinas de Turing cuyas cintas tienen varias ``pistas''. Pueden verse también como máquinas de varias cintas con movimientos ``sincronizados'': Movimiento que se hace en una cinta, se hace en todas.
Proposición 6.2
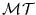
y
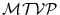
son equivalentes.
En efecto, por un lado, tenemos que toda máquina 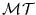 es en sí del tipo
es en sí del tipo
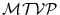 .
Recíprocamente, dada una máquina Mk del tipo
.
Recíprocamente, dada una máquina Mk del tipo
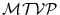 con k pistas, la podemos simular con una máquina M del tipo
con k pistas, la podemos simular con una máquina M del tipo 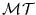 de cualquiera de las dos maneras alternativas:
de cualquiera de las dos maneras alternativas:
- 1.
- Si A es el alfabeto de Mk, entonces en cada momento el funcionamiento de Mk depende de la lista de k símbolos que aparece en la casilla actual, consistente de k casillas, una por cada pista. Esto define a una máquina del del tipo
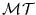 sobre el alfabeto Ak que es una potencia cartesiana del original.
sobre el alfabeto Ak que es una potencia cartesiana del original.
- 2.
- Consideremos una cinta de una sola pista en donde sus casillas se agrupan en bloques de k casillas. La posición j-ésima de la i-ésima pista en la cinta de Mk corresponde a la posición
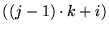 -ésima de la nueva cinta. En esta nueva, casillas contiguas en lamisma pista de Mk distanciarán de k casillas. El mecanismo de funcionamiento se modifica para que cada movimiento de Mk obligue a revisar un bloque de k casillas y haga la modificación correspondiente, trabajando siempre en bloques.
-ésima de la nueva cinta. En esta nueva, casillas contiguas en lamisma pista de Mk distanciarán de k casillas. El mecanismo de funcionamiento se modifica para que cada movimiento de Mk obligue a revisar un bloque de k casillas y haga la modificación correspondiente, trabajando siempre en bloques.
Máquinas con cintas de varias cintas,
 :
Estas son máquinas de Turing con varias cintas con movimientos ``independientes''.
:
Estas son máquinas de Turing con varias cintas con movimientos ``independientes''.
Proposición 6.3
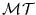
y
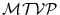
son equivalentes.
Demostraremos que
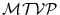 y
y
 son equivalentes.
En efecto, por un lado, tenemos que toda máquina
son equivalentes.
En efecto, por un lado, tenemos que toda máquina
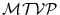 es en sí del tipo
es en sí del tipo
 .
Recíprocamente, dada una máquina
.
Recíprocamente, dada una máquina
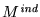 del tipo
del tipo
 con k pistas, la podemos simular con una máquina
con k pistas, la podemos simular con una máquina
 del tipo
del tipo
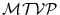 ,
con 2k pistas como sigue:
Cada cinta Cj da origen a dos pistas
Pj0,Pj1. La pista Pj1 tiene el mismo contenido que la cinta Cj. La pista Pj0 está en blanco salvo en la posición donde se encuentra la j-ésima cabeza lectora de
,
con 2k pistas como sigue:
Cada cinta Cj da origen a dos pistas
Pj0,Pj1. La pista Pj1 tiene el mismo contenido que la cinta Cj. La pista Pj0 está en blanco salvo en la posición donde se encuentra la j-ésima cabeza lectora de
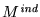 ,
en la cual hay una marca ``
,
en la cual hay una marca ``
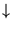 '' para marcar que ésa es la casilla escudriñada en la j-ésima cinta.
Con esto, la máquina
'' para marcar que ésa es la casilla escudriñada en la j-ésima cinta.
Con esto, la máquina
 se construye de manera inmediata.
Máquinas con dos símbolos,
se construye de manera inmediata.
Máquinas con dos símbolos,
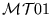 :
Estas son máquinas de Turing sobre el alfabeto (0+1).
:
Estas son máquinas de Turing sobre el alfabeto (0+1).
Proposición 6.4
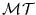
y
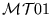
son equivalentes.
En efecto, por un lado, tenemos que toda máquina
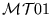 es en sí del tipo
es en sí del tipo 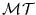 .
Recíprocamente, dada una máquina M del tipo
.
Recíprocamente, dada una máquina M del tipo 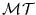 sobre un alfabeto con m símbolos, sea
sobre un alfabeto con m símbolos, sea
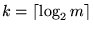 .
Cada símbolo en el alfabeto puede codificarse mediante una cadena de k bits. Por tanto M puede verse como una m''aquina de k pistas. De acuerdo con la segunda construcción de la máquina del tipo
.
Cada símbolo en el alfabeto puede codificarse mediante una cadena de k bits. Por tanto M puede verse como una m''aquina de k pistas. De acuerdo con la segunda construcción de la máquina del tipo 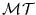 simuladora de una máquina del tipo
simuladora de una máquina del tipo
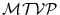 ,
obtenemos una máquina del tipo
,
obtenemos una máquina del tipo
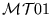 que simula a M.
que simula a M.




Siguiente: Computabilidad-Turing
Un nivel arriba: Máquinas de Turing
Anterior: Computaciones en máquinas de
Guillermo Morales-Luna
2000-07-10