



Siguiente: Problemas de acceso
Un nivel arriba: Complejidad en redes de
Anterior: Ejemplo
Sea R una r.P.g. y sea
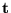 un marcado inicial. Un árbol de recubrimiento
un marcado inicial. Un árbol de recubrimiento
 describe las ``computaciones'' derivables por la red a partir del marcado inicial. Formalmente este árbol se define de manera inductiva:
describe las ``computaciones'' derivables por la red a partir del marcado inicial. Formalmente este árbol se define de manera inductiva:
- 1.
- La raíz se etiqueta con el marcado inicial
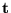 .
.
- 2.
- Si
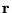 es un nodo ya construído con etiqueta
es un nodo ya construído con etiqueta
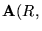 pueden ocurrir cuatro casos:
pueden ocurrir cuatro casos:
- (a)
- Ninguna transición es disparable con
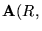 :
En este caso,
:
En este caso,
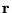 es una hoja de terminación muerta.
es una hoja de terminación muerta.
- (b)
- El marcado actual se ha repetido previamente: Si existe un ancestro
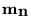 de
de
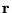 con la misma etiqueta, es decir, tal que
con la misma etiqueta, es decir, tal que
 ,
entonces
,
entonces
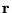 es una hoja de terminación ciclada-
es una hoja de terminación ciclada-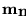 ,
y se coloca un apuntador-
,
y se coloca un apuntador-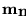 de
de
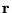 a
a
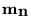 .
.
- (c)
- El marcado actual cubre propiamente a uno aparecido previamente: Si existe un ancestro
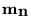 de
de
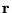 tal que
tal que
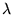 ,
entonces
,
entonces
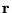 es una hoja de terminación ciclada-
es una hoja de terminación ciclada-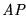 ,
y se coloca un apuntador-
,
y se coloca un apuntador-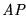 de
de
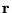 a
a
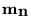 .
.
- (d)
- En cualquier otro caso, para cada transición t disparable se le asocia a
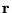 un nodo hijo etiquetado por el marcado
un nodo hijo etiquetado por el marcado
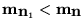 .
El arco hacia el hijo se etiqueta con la transición t.
.
El arco hacia el hijo se etiqueta con la transición t.
Las siguientes observaciones son inmediatas
- 1.
- Dados R y
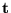 ,
,
 es efectivamente constructible.
es efectivamente constructible.
- 2.
- Cada nodo en
 tiene a lo sumo un número finito de hijos. Luego, si el árbol fuera infinito, necesariamente ha de tener ramas infinitas.
tiene a lo sumo un número finito de hijos. Luego, si el árbol fuera infinito, necesariamente ha de tener ramas infinitas.
- 3.
- Por lo anterior, se tiene que todo árbol
 es finito.
es finito.
- 4.
- Si
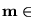 aparece como etiqueta de un nodo entonces cae en
aparece como etiqueta de un nodo entonces cae en
 .
.
Proposición: Se puede decidir efectivamente si acaso la red R es acotada.
Demostración: La red R es acotada si y sólo si
 no posee hojas de terminación ciclada-
no posee hojas de terminación ciclada-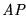 .
.
Consecuencias: Con técnicas similares a la anterior resulta que los conceptos siguientes son todos efectivamente decidibles:
- 1.
- Disparabilidad potencial de transiciones.
- 2.
- Para cada transición t, la mortalidad-t de marcados.
- 3.
- Disparabilidad infinita de una transición.
- 4.
- Para cada lugar l, el acceso a marcados que lo hagan asumir marcas positivas (llegadas de estafetas).




Siguiente: Problemas de acceso
Un nivel arriba: Complejidad en redes de
Anterior: Ejemplo
Guillermo Morales-Luna
2000-07-10
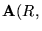 :
En este caso,
:
En este caso,
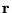 es una hoja de terminación muerta.
es una hoja de terminación muerta.
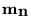 de
de
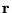 con la misma etiqueta, es decir, tal que
con la misma etiqueta, es decir, tal que
 ,
entonces
,
entonces
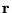 es una hoja de terminación ciclada-
es una hoja de terminación ciclada-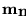 ,
y se coloca un apuntador-
,
y se coloca un apuntador-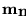 de
de
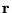 a
a
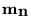 .
.
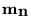 de
de
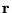 tal que
tal que
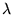 ,
entonces
,
entonces
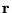 es una hoja de terminación ciclada-
es una hoja de terminación ciclada-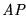 ,
y se coloca un apuntador-
,
y se coloca un apuntador-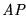 de
de
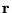 a
a
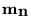 .
.
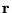 un nodo hijo etiquetado por el marcado
un nodo hijo etiquetado por el marcado
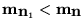 .
El arco hacia el hijo se etiqueta con la transición t.
.
El arco hacia el hijo se etiqueta con la transición t.
 describe las ``computaciones'' derivables por la red a partir del marcado inicial. Formalmente este árbol se define de manera inductiva:
describe las ``computaciones'' derivables por la red a partir del marcado inicial. Formalmente este árbol se define de manera inductiva: