



Siguiente: Problema de acceso generalizado
Un nivel arriba: Complejidad en redes de
Anterior: Problemas de acotación
Para una r.P.g.
R=(L,T,A,p) y un marcado inicial
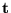 ,
consideremos los problemas siguientes:
Problema de acceso (PA):
,
consideremos los problemas siguientes:
Problema de acceso (PA):
Instancia:
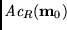
Solución:
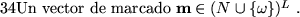
Problema de acceso a submarcados (PAS):
Instancia:
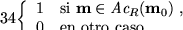
Solución:
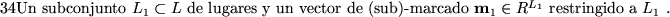
Problema de acceso a cero (PA0): PA con la instancia
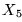 .
Problema de acceso a cero en un lugar dado (PA0L):
.
Problema de acceso a cero en un lugar dado (PA0L):
Instancia:
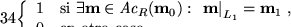
Solución:
![\begin{pagi}{34}$\left\{\begin{array}{ll}
1 &\mbox{\rm si $\exists\mbox{\bf m}\...
...ht]_{l}=0$ , } \\
0 &\mbox{\rm en otro caso. }
\end{array}\right.$\end{pagi}](img2109.gif)
Se ve directamente que valen las reducibilidades siguientes:
Para completar el diagrama de reducibilidades veamos lo siguiente:
- PAS se reduce a PA0:
- Dada una instancia de PAS consistente de una red
R=(L,T,A,p), un marcado inicial
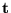 ,
un subconjunto
,
un subconjunto
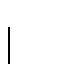 de lugares y un vector de (sub)-marcado
de lugares y un vector de (sub)-marcado
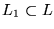 la transformaremos en una instancia equivalente de PA0.
Introducimos como elementos nuevos
la transformaremos en una instancia equivalente de PA0.
Introducimos como elementos nuevos
Se ve que la instancia transformada tiene una solución positiva en PA0 si y sólo si la instancia dada tiene también una solución positiva en PAS.
- PA0 se reduce a PA0L:
- Dada una instancia de PA0 consistente de una red
R=(L,T,A,p) y un marcado inicial
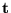 ,
añadimos un lugar nuevo
,
añadimos un lugar nuevo 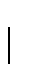 tal que en todo marcado accesible
tal que en todo marcado accesible
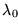 se tenga
se tenga
Así tendremos que la instancia dada da respuesta positiva con PA0 si y sólo si la instancia modificada la da con PA0L para 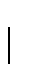 .
Para esto, inicialmente se le asigna a
.
Para esto, inicialmente se le asigna a 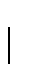 una marca de
una marca de
![$\sum_{l\in L}\left[\mbox{\bf m}_0\right]_{l}$](img2117.gif) .
Luego, para cada transición
.
Luego, para cada transición 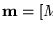 calculamos el cambio de marcas cuando se dispara t:
calculamos el cambio de marcas cuando se dispara t:
Dependiendo de este valor se hacen conexiones a 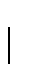 :
:
Así pues, los cuatro problemas anteriores de acceso son reducibles unos a otros.




Siguiente: Problema de acceso generalizado
Un nivel arriba: Complejidad en redes de
Anterior: Problemas de acotación
Guillermo Morales-Luna
2000-07-10
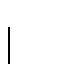 de lugares y un vector de (sub)-marcado
de lugares y un vector de (sub)-marcado
![$\sum_{l\in L}\left[\mbox{\bf m}_0\right]_{l}$](img2117.gif) .
Luego, para cada transición
.
Luego, para cada transición