



Siguiente: Algoritmos probabilísticos y su
Un nivel arriba: Problemas de acceso
Anterior: Problemas de acceso
Sea
 .
Consideremos el siguiente
Problema de acceso a A (
.
Consideremos el siguiente
Problema de acceso a A (
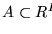 ):
):
Instancia:
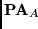
Solución:
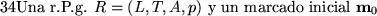
A es resoluble por acceso si
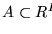 se reduce a PA.
Se tiene,
se reduce a PA.
Se tiene,
- 1.
- Todo conjunto accesible es por sí mismo resoluble por acceso.
- 2.
- Problema del marcado común: La intersección de dos conjuntos resolubles por acceso es también resoluble por acceso.
- 3.
- La unión finita de conjuntos resolubles por acceso es también resoluble por acceso.
- 4.
- Todo conjunto lineal, es decir, toda imagen de una transformación afín,
es resoluble por acceso.
- 5.
- Todo conjunto semilineal, es decir, expresable como la unión finita de conjuntos lineales, es resoluble por acceso.
- 6.
- Soluciones de ecuaciones diofantinas lineales y poliedros son resolubles por acceso.
Guillermo Morales-Luna
2000-07-10
 .
Consideremos el siguiente
Problema de acceso a A (
.
Consideremos el siguiente
Problema de acceso a A (