



Siguiente: Tesis de Church
Un nivel arriba: Máquinas de Turing
Anterior: Modelos restringidos de máquinas
Una función
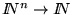 se dice ser computable-T, o computable-Turing, si existe una máquina de Turing que la calcula.
Aunque básicamente es correcta esta definición, es evidente que quedan algunos elementos en ella que aún no han sido precisados.
Antes que nada, consideraremos en esta sección que los números naturales se están representando en base 2, utilizando únicamente a los dígitos 0,1. Consideraremos también al menos dos símbolos más: la coma ``,'' para separar números, y el ``blanco'', ``b'', para marcar en su totalidad, salvo un número finito de casillas, a la cinta de cualquier máquina de Turing. Así, por ejemplo, el vector (1,2,3) se representa por la cadena b1,10,11b. Sea
se dice ser computable-T, o computable-Turing, si existe una máquina de Turing que la calcula.
Aunque básicamente es correcta esta definición, es evidente que quedan algunos elementos en ella que aún no han sido precisados.
Antes que nada, consideraremos en esta sección que los números naturales se están representando en base 2, utilizando únicamente a los dígitos 0,1. Consideraremos también al menos dos símbolos más: la coma ``,'' para separar números, y el ``blanco'', ``b'', para marcar en su totalidad, salvo un número finito de casillas, a la cinta de cualquier máquina de Turing. Así, por ejemplo, el vector (1,2,3) se representa por la cadena b1,10,11b. Sea
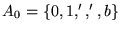 el alfabeto consistente de esos cuatro símbolos.
Dado
el alfabeto consistente de esos cuatro símbolos.
Dado
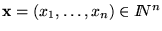 la representación de
la representación de
 es
es
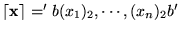 donde para cada número
donde para cada número
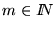 ,
(m)2 es la representación binaria de m. Aunque
,
(m)2 es la representación binaria de m. Aunque
 y
y
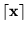 son dos entes distintos (uno es un objeto, un vector, y el otro es la representación de ese objeto), en la práctica los confundiremos y no haremos más distinción entre objetos y sus representaciones.
Sea A un alfabeto que contenga a A0 y sea M una máquina de Turing sobre A con estado inicial q0. Sea
son dos entes distintos (uno es un objeto, un vector, y el otro es la representación de ese objeto), en la práctica los confundiremos y no haremos más distinción entre objetos y sus representaciones.
Sea A un alfabeto que contenga a A0 y sea M una máquina de Turing sobre A con estado inicial q0. Sea
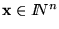 .
Por
.
Por
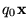 denotamos a la descripción instantánea que dice que el contenido de la cinta de la máquina de Turing es la representación del vector
denotamos a la descripción instantánea que dice que el contenido de la cinta de la máquina de Turing es la representación del vector
 ,
que el estado actual de la máquina es el inicial q0 y que se está escudriñando la casilla más a la izquierda de
,
que el estado actual de la máquina es el inicial q0 y que se está escudriñando la casilla más a la izquierda de
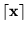 que no está en blanco. Si q es un estado final, con la notación
que no está en blanco. Si q es un estado final, con la notación
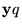 designaremos la situación de que la máquina ha arribado al estado q y la cadena de 0's, 1's y comas inmediatamente a la izquierda de la casilla escudriñada corresponde a un vector de números naturales.
Escribiremos
designaremos la situación de que la máquina ha arribado al estado q y la cadena de 0's, 1's y comas inmediatamente a la izquierda de la casilla escudriñada corresponde a un vector de números naturales.
Escribiremos
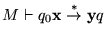 para indicar que mediante computaciones legales de M, partiendo de la descripción instantánea
para indicar que mediante computaciones legales de M, partiendo de la descripción instantánea
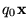 ,
en algún momento se deriva la descripción
,
en algún momento se deriva la descripción
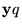 .
En tal caso, escribimos
.
En tal caso, escribimos
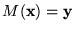 .
Si la máquina no se para a partir de
.
Si la máquina no se para a partir de
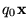 escribiremos
escribiremos
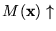 .
La función que calcula M es
.
La función que calcula M es
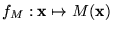 .
Así pues, una función
.
Así pues, una función
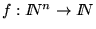 es computable-T si y sólo si existe una máquina de Turing sobre un alfabeto
es computable-T si y sólo si existe una máquina de Turing sobre un alfabeto
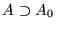 tal que f=fM.
Comparemso pues las nociones de computabilidad introducidas hasta ahora:
tal que f=fM.
Comparemso pues las nociones de computabilidad introducidas hasta ahora:
Lema 6.1
Toda función computable-T es computable (mediante programas-while ).
La demostración formal de este lema puede ser muy engorrosa y acaso poco ilustrativa. Lo que hay que ver, en esencia, es que el programa de cualquier máquina de Turing, es decir, su mecanismo de control visto como una lista de quíntuplas, puede ser convertido en un programa-while . En otras palabras, lo que hay que ver es que toda máquina de Turing puede ser simulada por un programa-while . Lo que no es otra cosa sino que las máquinas de Turing pueden ser programables en el marco de la programación-while . Cualquier programador con experiencia media quedará convencido de que esto último, en efecto, sí es posible.
Recíprocamente, se tiene
Lema 6.2
Toda función computable es computable-T.
En efecto, observemos las reglas que definen a los programas-while en la figura (1.6). Primeramente observamos que el decidir si acaso el contenido de una variable es nulo o no lo podemos hacer con máquinas de Turing. También mediante ellas podemos calcular a las funciones x++ y x-.
Ahora es claro que dadas dos máquinas de Turing M1 y M2, se puede construir una tercera máquina de Turing M3 tal que, para cualquier posible entrada
 se tiene
se tiene
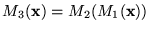 .
Por tanto, si los programas-while P1 y P2 fueran simulados por las máquinas de Turing M1 y M2 entonces la concatenación P1;P2 se simula por M3. En otras palabras, la clase de máquinas de Turing es cerrada bajo composición.
También, tenemos que si el programa-while P1 fuese simulado por una máquina de Turing M entonces el esquema
.
Por tanto, si los programas-while P1 y P2 fueran simulados por las máquinas de Turing M1 y M2 entonces la concatenación P1;P2 se simula por M3. En otras palabras, la clase de máquinas de Turing es cerrada bajo composición.
También, tenemos que si el programa-while P1 fuese simulado por una máquina de Turing M entonces el esquema
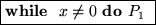 se puede también simular por una máquina de Turing.
De ambos lemas, obtenemos,
se puede también simular por una máquina de Turing.
De ambos lemas, obtenemos,
Teorema 6.1
Las nociones de computabilidad-Turing y computabilidad (mediante programas-while ) coinciden.




Siguiente: Tesis de Church
Un nivel arriba: Máquinas de Turing
Anterior: Modelos restringidos de máquinas
Guillermo Morales-Luna
2000-07-10