



Siguiente: Presentación de la teoría
Un nivel arriba: Complejidad de Kolmogorov
Anterior: Complejidad de Kolmogorov
La información contenida en una cadena de caracteres la podemos representar como la longitud del programa mínimo para construirla.
- 1n se construye con un programa de longitud
 .
.
-
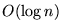 se construye con un programa de longitud O(1).
se construye con un programa de longitud O(1).
Conforme la cadena dada sea más ``regular'', tanto más ``comprimible'' ha de ser: Un programa que la construya será muy compacto.
Así pues la noción de ``aleatoriedad'' puede identificarse como ``no-compresibilidad''.
Definición: Una sucesión
es un colectivo si
- 1.
- La probabilidad de aparición de 1 en la sucesión está bien definida:
- 2.
- Dada una función
 definamos la sucesión
definamos la sucesión
haciendo
Pues bien, para la noción de ``colectivo'' hemos de tener también que para todo 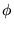 ,
en una clase de funciones dada, por ejemplo, la clase de funciones recursivas totales,
,
en una clase de funciones dada, por ejemplo, la clase de funciones recursivas totales,
Ejemplo: Sea
 una sucesión tal que satisface la primera condición anterior:
una sucesión tal que satisface la primera condición anterior:
Consideremos la función
Si se cumpliera la segunda condición, hemos de tener p=1.
Sin embargo para la función
hemos de tener que p=0.
Así pues en clases grandes de funciones la definición anterior no se puede satisfacer.




Siguiente: Presentación de la teoría
Un nivel arriba: Complejidad de Kolmogorov
Anterior: Complejidad de Kolmogorov
Guillermo Morales-Luna
2000-07-10
 .
.
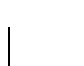 .
.
 definamos la sucesión
definamos la sucesión
 una sucesión tal que satisface la primera condición anterior:
una sucesión tal que satisface la primera condición anterior: