Siguiente: Definiciones básicas Un nivel arriba: Complejidad de Kolmogorov Anterior: Introducción

Presentación de la teoría

Identificaremos a N con $\{0,1\}^{<\omega}$ mediante la correspondencia

$$\begin{eqnarray*}x:N &\rightarrow& \{0,1\}^{<\omega} \\ n &\mapsto& x(n) \end{eqnarray*}$$

donde

$$x(n)=\left\{\begin{array}{ll} \mbox{\it nil} & \mbox{\rm si ... ... $n>0$, con }k=\lfloor \log_2(n+1) \rfloor. \end{array}\right.$$

((n)_2,k es la representación en base 2 de n utilizando exactamente k bits). En la Figura 1 presentamos esta correspondencia. Cada entrada es de la forma $\frac{x(n)}{n}$.

 

Figure: Correspondencia $N\rightarrow \{0,1\}^{<\omega }$.

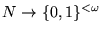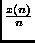x(n) es pues una cadena de longitud $O(\log(n))$.


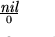La función inversa es

$$\begin{eqnarray*}n:\{0,1\}^{<\omega} &\rightarrow& N \\ x &\mapsto& n(x) \end{eqnarray*}$$

Denotemos por |x| a la longitud de la cadena x. Resulta claro que

n(x)=2^|x|-1+(x)₂.

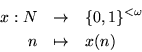
Esta última función es un programa universal S que dado el código p, como una cadena en $\{0,1\}^{<\omega}$, da el número n. La complejidad de Kolmogorov de una cadena x es la longitud del mínimo programa p que reconstruye a x:

$$K_S(x)=\mathop{\rm Min}\{\vert p\vert:S(p)=n(x)\}.$$