Siguiente: Descripciones auto-delimitadoras Un nivel arriba: Incomprimibilidad Anterior: Incomprimibilidad

Ejemplos y observaciones

1. Sea x de la forma x=uvw, donde v es una partícula comprimible,

K(v)<|v|.

Entonces v no puede comprimirse demasiado. En efecto, a x lo podemos recosntruir mediante

• una descripción de |u|,
• una descripción de uw,
• separadores de las dos descripciones anteriores.

Luego

$$K(x)\leq K(v)+O(\log\vert x\vert)+\vert uw\vert.$$

Como $\vert x\vert\leq K(x)$ se tiene

$$K(v)\geq \vert v\vert-O(\log\vert x\vert).$$

Una cadena incomprimible puede tener cadenas comprimibles (pero no tanto). Esto es similar al hecho de que una cadena aleatoria de 0's y 1's contiene cadenas constantes de longitud arbitraria.


2. Para cada objeto x sea p(x) un programa mínimo que genera a x. Entonces p(x) es en sí incomprimible. De hecho existe c tal que

$$K(p(x))\geq \vert p(x)\vert-c\;forall x.$$

En efecto, supongamos lo contrario. Entonces

$$\forall x\;\exists c_x:\;K(p(x))\leq \vert p(x)\vert-c_x.$$

Sea U una máquina universal de referencia y sea V=U². Entonces

$$\forall x:\;V(p(p(x)))=x.$$

Luego

$$\begin{eqnarray*}K(x) &=& K(p(p(x)) \\ &\leq& \vert p(p(x))\vert-c_{p(x)} \\ &\leq& \vert p(x)\vert-c_{x,*}+n(V)+1 \end{eqnarray*}$$

lo cual es absurdo pues necesariamente K(x)=|p(x)|.


Sea $g:N\rightarrow N$. Diremos que una cadena x es g-incomprimible si

$$K(x)\geq n(x)-g(n(x)).$$

Para cada n, la razón entre los objetos comprimibles respecto a todos los de longitud n es

$$\frac{2^{n-g(n)}-1}{2^n}\approx 2^{-g(n)}$$

lo que converge a cero si g es creciente. Los objetos 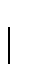$\log$-comprimibles se dicen ser aleatorios.


Si x es una sucesión de longitud infinita, x es g-incomprimible si para cada n es segmento inicial de longitud n lo es:

$$\forall n: K(x[0,n-1])\geq n-g(n).$$

Siguiente: Descripciones auto-delimitadoras Un nivel arriba: Incomprimibilidad Anterior: Incomprimibilidad