



Siguiente: Estimaciones de la complejidad
Un nivel arriba: Presentación de la teoría
Anterior: Ejemplos y observaciones
Consideremos la función
definida inductivamente como sigue:
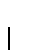 se obtiene de intercalar un 0 entre cualesquiera dos símbolos de x y finalizar con un 1.
La cadena
se obtiene de intercalar un 0 entre cualesquiera dos símbolos de x y finalizar con un 1.
La cadena
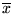 se dice ser la versión autodelimitadora de x. Si la longitud de x es n la longitud de
se dice ser la versión autodelimitadora de x. Si la longitud de x es n la longitud de 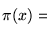 es
es
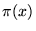 .
Una cadena de cadenas
.
Una cadena de cadenas
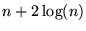 se codifica yuxtaponiendo a los códifos:
se codifica yuxtaponiendo a los códifos:
Guillermo Morales-Luna
2000-07-10