



Siguiente: Propiedades
Un nivel arriba: Kolmogorov
Anterior: Kolmogorov
Sea A un conjunto. Definamos
A es ralo si
Lema 1: Si A es un conjunto recursivo y ralo entonces para cada constante c se tiene que sólo para un número finito de elementos x se cumple
Lema 2: Sea A es un conjunto recursivo enumerable y
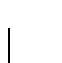 .
Si
.
Si
entonces para cada constante c se tiene que sólo para un número finito de elementos x se cumple
Lema 3: Sea A es un conjunto recursivo enumerable. Si
donde p(X) es un polinomio,
entonces para cada constante c se tiene que sólo para un número finito de elementos x se cumple
Guillermo Morales-Luna
2000-07-10
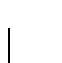 .
Si
.
Si