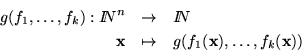Siguiente: Esquema de minimización
Un nivel arriba: Propiedades de cerradura de
Anterior: Propiedades de cerradura de
Este esquema es la composición típica de funciones. Dada una función de k argumentos y dadas k funciones, de n argumentos cada una, al componer a las segundas con la primera obtenemos una función de n argumentos,
Si
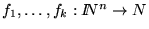 son k funciones y
son k funciones y
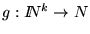 es otra función, la composición de las f's con la g es la función
es otra función, la composición de las f's con la g es la función
Así pues,
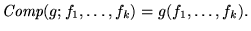
Guillermo Morales-Luna
2000-07-10