Siguiente: Esquema de minimización acotada Un nivel arriba: Propiedades de cerradura de Anterior: Esquema de composición

Esquema de minimización

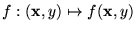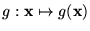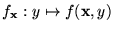Dada una función $f:(\mbox{\bf x},y)\mapsto f(\mbox{\bf x},y)$ de n+1 argumentos podemos construir una nueva función $g:\mbox{\bf x}\mapsto g(\mbox{\bf x})$ asociándole a cada $\mbox{\bf x}$ el mínimo y para el cual se anula la sección $f_{\mbox{\scriptsize\bf x}}:y\mapsto f(\mbox{\bf x},y)$ de f a la altura $\mbox{\bf x}$. g se obtiene de minimizar a f. Así pues, este esquema toma una función de n+1 argumentos y produce otra de n argumentos,

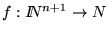Más precisamente: Si $f:I\!\!N^{n+1}\rightarrow N$ es una función total, es decir, definida en todos las posibles instancias a sus argumentos, definimos

$$\begin{eqnarray*}(\mu_y {[f=0]}):I\!\!N^n &\rightarrow& I\!\!N\\ \mbox{\bf x} ... ...$y$ ,} \\ \perp &\mbox{\rm en otro caso.} \end{array}\right. \end{eqnarray*}$$

Así pues, $\mbox{\it Mini}(f)=(\mu_y {[f=0]}).$