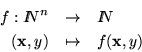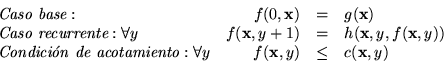Siguiente: Computabilidad de los esquemas
Un nivel arriba: Propiedades de cerradura de
Anterior: Esquema de recursión
Este esquema es similar al anterior, con la sola excepción de que los valores de la función que se define recurrentemente no excedan los de una tercera función dada,
Más precisamente:
Si
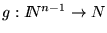 ,
,
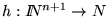 y
y
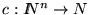 son tres funciones definimos
son tres funciones definimos
donde
Así pues,
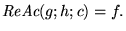
Guillermo Morales-Luna
2000-07-10