Siguiente: Esquema de recursión acotada
Un nivel arriba: Propiedades de cerradura de
Anterior: Esquema de minimización acotada
Una típica aplicación de este esquema define a una función f haciendo
La función g está definiendo el caso ``base'' de la recurrencia, en tanto que la función h define precisamente el recurrente. En h, puede también ocurrir y como un argumento. Así pues, este esquema se aplica sobre dos funciones, la primera correspondiente al caso ``base'' con n-1 argumentos y la segunda correspondiente al caso recurrente con n+1 argumentos, y produce una función con n argumentos,
Más precisamente:
Si
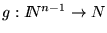 y
y
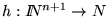 son dos funciones definimos
son dos funciones definimos
donde
Así pues,
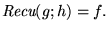
Guillermo Morales-Luna
2000-07-10