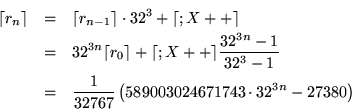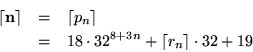Siguiente: Observaciones sobre la codificación Un nivel arriba: Codificación de programas-while Anterior: Codificación de símbolos

Codificación de programas y tiras de símbolos

Cada palabra P, en el alfabeto de los programas-while , se codifica por el número cuya representación binaria coincide con la yuxtaposición de los códigos de los símbolos en las palabras. Esto define una función

$$\lceil\cdot\rceil:\mbox{\rm programas-{\bf while }}\rightarrow N.$$

Ejemplos: 1. $\lceil ;X++ \rceil=(11010\;10111\;10100)_2 = 27380$.

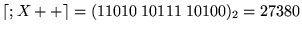2. $\begin{array}[t]{lcl} \lceil r_0\rceil &=& \lceil\mbox{\rm {\bf while }$x\not=... ...\;10111\;10110\;11000\;10001\;10111\;10101)_2 \\ &=& 17975494389 \end{array}$

3. $\begin{array}[t]{lcl} \lceil {\bf0}\rceil &=& \lceil p_0\rceil \\ &=& 18\cdot 32^8+\lceil r_0\rceil\cdot 32 + 19 \\ &=& 1193691111091 \end{array}$

4. De manera recursiva, tenemos $\forall n>0$:

$$\begin{eqnarray*}\lceil r_n\rceil &=& \lceil r_{n-1}\rceil\cdot 32^3+\lceil ;X++... ...tstyle 32767}}\left(589003024671743\cdot32^{3 n} - 27380\right) \end{eqnarray*}$$

y

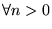$$\begin{eqnarray*}\lceil {\bf n}\rceil &=& \lceil p_n\rceil \\ &=& 18\cdot 32^{8+3n}+\lceil r_n\rceil\cdot 32+ 19 \end{eqnarray*}$$

Así se tiene que los códigos de los primeros 6 numerales son:

$$\begin{array}{ccr} \lceil {\bf0}\rceil &=& 1193691111091 \\ ... ...5}\rceil &=& 769421786917225345914194621564280467 \end{array}$$