



Siguiente: Primera lista de ejercicios
Un nivel arriba: Codificación de programas-while
Anterior: Codificación de programas y
Denotemos por
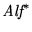 al conjunto de tiras sobre el alfabeto de los programas-while .
al conjunto de tiras sobre el alfabeto de los programas-while .
- 1.
-
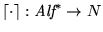 es una función
es una función
- (a)
- efectivamente calculable, es decir, dada una tira cualquiera
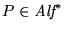 se obtiene de manera procedimental su código
se obtiene de manera procedimental su código
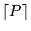 ,
,
- (b)
- inyectiva, pues para que
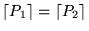 es necesario que P1=P2, cualesquiera que sean las tiras
es necesario que P1=P2, cualesquiera que sean las tiras
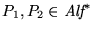 ,
y
,
y
- (c)
- que no es suprayectiva, pues la representación binaria de cualquier número en la imagen de
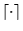 ha de tener una longitud que es un múltiplo de 5 y en cada posición múltiplo de 5, contada de derecha a izquierda, ha de estar ``prendido'' el bit correspondiente. En otras palabras, un número está en la imagen de
ha de tener una longitud que es un múltiplo de 5 y en cada posición múltiplo de 5, contada de derecha a izquierda, ha de estar ``prendido'' el bit correspondiente. En otras palabras, un número está en la imagen de
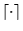 si y sólo si al escribir a ese número en base 32=25, sólo aparecen los dígitos que, en decimal, están entre 16 y 26 inclusive.
si y sólo si al escribir a ese número en base 32=25, sólo aparecen los dígitos que, en decimal, están entre 16 y 26 inclusive.
- 2.
- Puesto que la clase de los programas-while es un subconjunto propio de
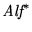 tenemos que el conjunto de códigos de programas-while ,
tenemos que el conjunto de códigos de programas-while ,
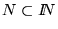 ,
es un subconjunto propio de la imagen de
,
es un subconjunto propio de la imagen de
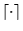 .
.
- 3.
- Sin embargo, dado
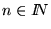 es algorítmicamente decidible si acaso existe un programa-while P tal que
es algorítmicamente decidible si acaso existe un programa-while P tal que
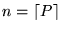 .
En efecto, dado n se puede calcular, mediante la ``división larga'' de enteros, la representación en base 32 de n y, obtenida ésta, hacer la conversión a una palabra
.
En efecto, dado n se puede calcular, mediante la ``división larga'' de enteros, la representación en base 32 de n y, obtenida ésta, hacer la conversión a una palabra
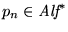 mediante la codificación descrita en la tabla 1.6. Luego, mediante un autómata de pila, se puede ver si acaso pn se ajusta a la gramática de los programas-while .
mediante la codificación descrita en la tabla 1.6. Luego, mediante un autómata de pila, se puede ver si acaso pn se ajusta a la gramática de los programas-while .
- 4.
- El procedimiento descrito en el punto anterior para obtener
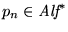 dado
dado
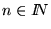 es un procedimiento efectivo para calcular la inversa de la codificación
es un procedimiento efectivo para calcular la inversa de la codificación
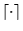 .
.
- 5.
- La codificación
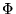 mencionada inmediatamente después de la observación 1.9.1 es, precisamente, la codificación
mencionada inmediatamente después de la observación 1.9.1 es, precisamente, la codificación
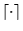 restringida a la clase de programas-while .
restringida a la clase de programas-while .
Para cada programa-while P, el número
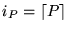 es el índice del programa P.
Consecuentemente, P se dice ser el iP-ésimo programa-while P=PiP.
Ahora bien, las funciones computables son las que se calculan mediante programas-while . Por tanto, podemos generalizar la noción de índice a las funciones computables como sigue:
es el índice del programa P.
Consecuentemente, P se dice ser el iP-ésimo programa-while P=PiP.
Ahora bien, las funciones computables son las que se calculan mediante programas-while . Por tanto, podemos generalizar la noción de índice a las funciones computables como sigue:
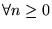 y para cada
y para cada 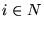 ,
el i-ésimo programa-while Pi calcula a la función
,
el i-ésimo programa-while Pi calcula a la función
donde y es el valor obtenido como sigue:
- 1.
- Si
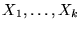 es la lista de variables de Pi, la instanciamos con
es la lista de variables de Pi, la instanciamos con
 ,
donde, en función de cómo se compare a n con k, la instanciación se hace como sigue:
,
donde, en función de cómo se compare a n con k, la instanciación se hace como sigue:
- 2.
- El valor que queda en la última variable Xk cuando termina Pi, si acaso terminare, es el asignado a y.
Si
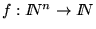 es computable y
f=f(n)i entonces i se dice ser un índice de f.
es computable y
f=f(n)i entonces i se dice ser un índice de f.
Proposición 9.1
Toda función computable tiene una infinidad de índices.
En efecto, sin entrar en minucias, tenemos que dos programas-while calculan a una misma función si, por ejemplo, uno posee variables ``mudas'', es decir, irrelevantes para el cálculo, que no aparecen en el otro, o bien si uno posee ``instrucciones ociosas'', digamos
(x++;x-;)* y, en lo demás, coincide con el otro programa.




Siguiente: Primera lista de ejercicios
Un nivel arriba: Codificación de programas-while
Anterior: Codificación de programas y
Guillermo Morales-Luna
2000-07-10
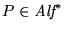 se obtiene de manera procedimental su código
se obtiene de manera procedimental su código
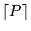 ,
,
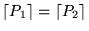 es necesario que P1=P2, cualesquiera que sean las tiras
es necesario que P1=P2, cualesquiera que sean las tiras
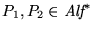 ,
y
,
y
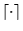 ha de tener una longitud que es un múltiplo de 5 y en cada posición múltiplo de 5, contada de derecha a izquierda, ha de estar ``prendido'' el bit correspondiente. En otras palabras, un número está en la imagen de
ha de tener una longitud que es un múltiplo de 5 y en cada posición múltiplo de 5, contada de derecha a izquierda, ha de estar ``prendido'' el bit correspondiente. En otras palabras, un número está en la imagen de
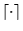 si y sólo si al escribir a ese número en base 32=25, sólo aparecen los dígitos que, en decimal, están entre 16 y 26 inclusive.
si y sólo si al escribir a ese número en base 32=25, sólo aparecen los dígitos que, en decimal, están entre 16 y 26 inclusive.
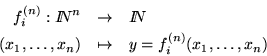
![\begin{displaymath}\begin{array}{l}
k\leq n:\forall j\leq k(X_j:=x_j) \vspace{2...
...X_j:=x_j)]\land[\forall j\in]\!]n,k]\!] (X_j:=0)].
\end{array}\end{displaymath}](img297.gif)