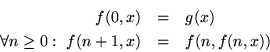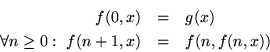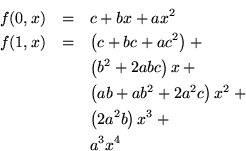Siguiente: Funciones elementales Un nivel arriba: Conceptos básicos Anterior: Conceptos básicos

Dos esquemas de reiteración

1.

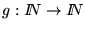Sea $g:I\!\!N\rightarrow I\!\!N$ una función recursiva primitiva. Definimos a la función 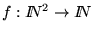$f:I\!\!N^2\rightarrow I\!\!N$ recursivamente como sigue

$$\begin{eqnarray*}f(0,x) &=& g(x) \\ \forall n\geq 0:\ f(n+1,x) &=& f(n,f(n,x)) \end{eqnarray*}$$

Mostremos que f es una función recursiva primitiva. Reescritura de f: Se puede ver que 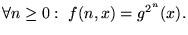$\forall n\geq 0:\ f(n,x)=g^{2^n}(x).$ Por tanto, se sigue que

2.

Si 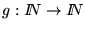$g:I\!\!N\rightarrow I\!\!N$ una función recursiva primitiva entonces

$$\mbox{\fbox{la {\em iteraci\'on} $h:(n,x)\mapsto g^n(x)$ es una funci\'on recursiva primitiva.} }$$

En efecto, f es una función recursiva primitiva porque es igual a la composición de una función recursiva primitiva con la función recursiva primitiva anterior.

Ejemplos Como ejemplos de la segunda función de reiteración arriba descrita la aplicaremos sobre algunas funciones polinomiales.

Sucesor

Supongamos g(x)=x+1. Entonces f(n,x)=x+2ⁿ.

Una lineal

Supongamos g(x)=2x+1. Entonces f(n,x)=2²ⁿ x+(2²ⁿ-1).

Caso lineal general

Supongamos g(x)=a x+b. Entonces

$$f(n,x)=a^{2^n} x+b\left(\frac{{\textstyle a^{2^n}-1}}{{\textstyle a-1}}\right).$$

Caso cuadrático general

Supongamos g(x)=a x²+bx + c. Entonces

$$\begin{eqnarray*}f(0,x) &=& c+ b x+ a x^2 \\ f(1,x) &=& \left(c + b c + a c^2\... ...ight) x^2 + \\ && \left(2 a^2 b\right) x^3 + \\ && a^3x^4 \end{eqnarray*}$$

Para el siguiente ``renglón'', los valores de f(2,x) se muestran en la tabla 2.1.

  

Table 2.1: Valores de f(2,x).