



Siguiente: Propiedades de la escala
Un nivel arriba: Jerarquía de Grzegorczyk
Anterior: Jerarquía de Grzegorczyk
Consideremos la sucesión
 definida como sigue:
definida como sigue:
| f0(x,y) |
= |
y+1 |
(1) |
| f1(x,y) |
= |
x+y |
(2) |
| f2(x,y) |
= |
(x+1)(y+1) |
(3) |
y para cada 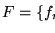 definimos inductivamente
definimos inductivamente
| fn(0,y) |
= |
fn-1(y+1,y+1) |
(4) |
 |
= |
fn(x-1,fn(x-1,y)) |
(5) |
La relación 2.4 indica que, en ``su primer renglón'', la n-ésima función asume los valores en la diagonal de la (n-1)-ésima, corridos una posición hacia adelante.
Ahora bien, hablando de manera tosca y ambigua en demasía, podríamos decir que la relación 2.5 indica que, en ``su x-ésimo renglón'', la n-ésima función está ``reiterando x veces los valores previos de esa misma n-ésima función''.
La primera función construída según 2.4 y 2.5, a saber, f3, tiene, en cada renglón, un crecimiento polinomial muy rápido en términos de y, pero, en cada columna, tiene un crecimiento doblemente exponencial en términos de x. En la tabla 2.3 presentamos las formas que asume f3(x,y) haciendo sustituciones para los primeros valores de x.
Table 2.3:
Formas de f3(x,y), con x=0,1,2,3.
![\begin{table}\begin{center}\fbox{\begin{minipage}[t]{40em}
\begin{eqnarray*}
f...
...) }^2} \right) }^2}
\end{eqnarray*}
\end{minipage}}\end{center}
\end{table}](img478.gif) |
De hecho, puede verse que, en general,
así pues f3(x,y) es un polinomio en y de grado 22x.
Por tanto, tendremos que
 Aquí ya es evidente que se carece de notación ``aritmética'' para escribir a
Aquí ya es evidente que se carece de notación ``aritmética'' para escribir a
 ,
ya sin decir más de
,
ya sin decir más de
 con
con  .
.
 toma los valores en la diagonal de f4 y reinicia el proceso.
Et cetera.
No es presuntuoso afirmar que el crecimiento de f10 o de f1998 o de
f19981998 supera, con mucho, los alcances de nuestro propio entendimiento.
toma los valores en la diagonal de f4 y reinicia el proceso.
Et cetera.
No es presuntuoso afirmar que el crecimiento de f10 o de f1998 o de
f19981998 supera, con mucho, los alcances de nuestro propio entendimiento.




Siguiente: Propiedades de la escala
Un nivel arriba: Jerarquía de Grzegorczyk
Anterior: Jerarquía de Grzegorczyk
Guillermo Morales-Luna
2000-07-10
 Aquí ya es evidente que se carece de notación ``aritmética'' para escribir a
Aquí ya es evidente que se carece de notación ``aritmética'' para escribir a