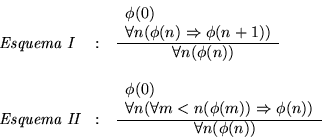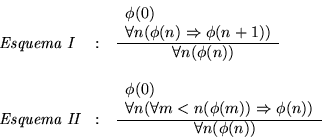Siguiente: Inducción recurrente
Un nivel arriba: Inducción matemática
Anterior: Inducción matemática
Sea 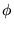 una fórmula con una variable libre x, definida en el lenguaje de la aritmética. Para demostrar la sentencia
una fórmula con una variable libre x, definida en el lenguaje de la aritmética. Para demostrar la sentencia
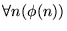 ,
un primer esquema de inducción verifica primero que se cumple
,
un primer esquema de inducción verifica primero que se cumple 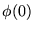 y luego, suponiendo que se cumple
y luego, suponiendo que se cumple 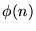 demuestra que se cumple
demuestra que se cumple 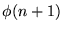 ;
un segundo esquema de inducción verifica primero que se cumple
;
un segundo esquema de inducción verifica primero que se cumple 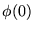 y luego, suponiendo que se cumple
y luego, suponiendo que se cumple 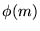 ,
para cualquier m<n, demuestra que se cumple
,
para cualquier m<n, demuestra que se cumple 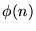 .
Estos esquemas, puestos como reglas de deducción quedan como sigue:
.
Estos esquemas, puestos como reglas de deducción quedan como sigue:
Teorema 2.1
Ambos esquemas son equivalentes.
En efecto:
- 1.
-
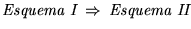 ): Supongamos válido el
): Supongamos válido el
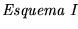 .
Sea
.
Sea 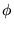 una fórmula tal que se cumplen
una fórmula tal que se cumplen
Mostremos primero que
Para esto usemos el
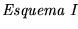 aplicado a la fórmula
aplicado a la fórmula
![$\phi_1(n)\equiv\left[\phi(0)\Rightarrow \forall m\leq n:\phi(m)\right]$](img61.gif) .
.
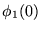 se cumple en virtud de que para cualquier fórmula
se cumple en virtud de que para cualquier fórmula 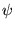 ,
la fórmula
,
la fórmula
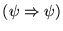 es un teorema del cálculo de predicados puro.
Ahora, supongamos que vale
es un teorema del cálculo de predicados puro.
Ahora, supongamos que vale 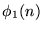 .
Hemos de probar que vale
.
Hemos de probar que vale
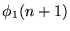 .
Supongamos
.
Supongamos 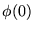 .
Por
.
Por 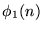 se tiene que es válido
se tiene que es válido
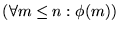 .
Por (*) se cumple también
.
Por (*) se cumple también 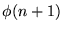 .
Así pues, la fórmula
.
Así pues, la fórmula
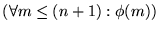 es válida, con lo cual se ve que, en efecto, la fórmula
es válida, con lo cual se ve que, en efecto, la fórmula
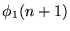 se cumple.
Demostremos ahora que vale
se cumple.
Demostremos ahora que vale
![$\forall n\left[\phi(n)\Rightarrow \phi(n+1)\right]$](img69.gif) .
Dado un n cualquiera, suponiendo que se cumple
.
Dado un n cualquiera, suponiendo que se cumple 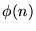 ,
puesto que
,
puesto que 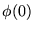 es cierto, se cumple por (**) que
es cierto, se cumple por (**) que
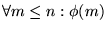 y por (*) resulta ya demostrado
y por (*) resulta ya demostrado 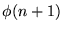 .
Por el Esquema I, resulta como una consecuencia
.
Por el Esquema I, resulta como una consecuencia
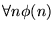 .
Tenemos pues que se cumple el Esquema II.
.
Tenemos pues que se cumple el Esquema II.
- 2.
-
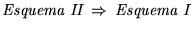 ): Supongamos válido el
): Supongamos válido el
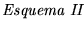 .
Sea
.
Sea 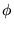 una fórmula tal que se cumplen
una fórmula tal que se cumplen
Resulta evidente que se cumple la fórmula
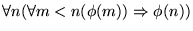 ,
pues, para cada n>0 la condición
,
pues, para cada n>0 la condición
![$[\forall m<n: \phi(m)]$](img76.gif) subsume a la fórmula
subsume a la fórmula 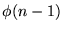 ,
la cual, de acuerdo con la segunda fórmula en (*) de este apartado implica
,
la cual, de acuerdo con la segunda fórmula en (*) de este apartado implica 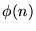 .
Por el Esquema II, resulta como una consecuencia
.
Por el Esquema II, resulta como una consecuencia
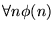 .
Tenemos pues que se cumple también el Esquema I.
.
Tenemos pues que se cumple también el Esquema I.




Siguiente: Inducción recurrente
Un nivel arriba: Inducción matemática
Anterior: Inducción matemática
Guillermo Morales-Luna
2000-07-10