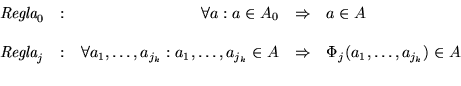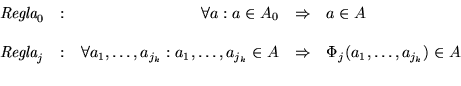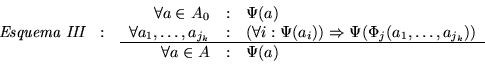Siguiente: Enumeración de Cantor
Un nivel arriba: Inducción matemática
Anterior: Inducción numérica
Este esquema se utiliza para demostrar predicados cuantificados universalmente definidos sobre conjuntos determinados constructivamente de manera recurrente.
Sea T un conjunto numerable.
Sea
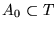 un conjunto inicial. Supongamos
un conjunto inicial. Supongamos
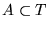 definido recurrentemente con las reglas siguientes:
definido recurrentemente con las reglas siguientes:
para
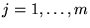 ,
donde cada función
,
donde cada función
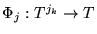 es, en la práctica, una regla de composición.
Para todo predicado
es, en la práctica, una regla de composición.
Para todo predicado 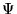 se tiene el esquema de demostración siguiente:
se tiene el esquema de demostración siguiente:
Como un ejemplo de construcción mediante este tipo de reglas, consideremos al siguiente:
Ejemplo. Sea T el conjunto formado por las palabras (de longitud finita) sobre el alfabeto (0+1), i.e. T=(0+1)*. Definimos el conjunto de palabras 0-preponderadas de manera recurrente como sigue:
El conjunto
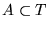 de palabras 0-preponderadas se ajusta a la construcción anterior, donde
de palabras 0-preponderadas se ajusta a la construcción anterior, donde
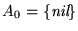 consta únicamente de la palabra vacía y hay dos reglas de composición
consta únicamente de la palabra vacía y hay dos reglas de composición 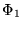 ,
,
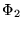 dadas por sendas reglas.
Más adelante veremos que una palabra es 0-preponderada si cualquier prefijo de ella posee más ceros que unos.
dadas por sendas reglas.
Más adelante veremos que una palabra es 0-preponderada si cualquier prefijo de ella posee más ceros que unos.
Proposición 2.1
El esquema III se prueba mediante el esquema II por inducción en el número de reglas para generar un elemento en A.
En efecto, con la notación utilizada en la formulación del Esquema III, sea
Como A se define únicamente por las reglas enlistadas, la fórmula
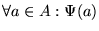 es lógicamente equivalente a la fórmula
es lógicamente equivalente a la fórmula
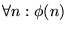 .
Mostremos pues que esta última es válida a partir de las hipótesis
.
Mostremos pues que esta última es válida a partir de las hipótesis
La primera de estas ecuaciones equivale a 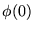 .
La segunda es claramente equivalente a
.
La segunda es claramente equivalente a
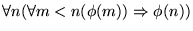 .
Por el Esquema II tenemos que se cumple
.
Por el Esquema II tenemos que se cumple
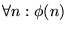 ,
y con esto queda demostrado el Esquema III.
,
y con esto queda demostrado el Esquema III.
Ejemplo. Retomando nuestro ejemplo anterior, sea A el conjunto de palabras 0-preponderadas. Sea
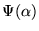 la proposición
la proposición
Procedamos de acuerdo con el Esquema III para ver que
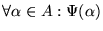 .
Inicialmente tenemos, trivialmente, que para la palabra vacía se cumple
.
Inicialmente tenemos, trivialmente, que para la palabra vacía se cumple 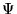 ,
es decir, vale
,
es decir, vale 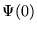 .
Ahora, de manera inductiva:
.
Ahora, de manera inductiva:




Siguiente: Enumeración de Cantor
Un nivel arriba: Inducción matemática
Anterior: Inducción numérica
Guillermo Morales-Luna
2000-07-10