



Siguiente: Funciones de apareamiento y
Un nivel arriba: Funciones recursivas primitivas
Anterior: Función de Ackermann
1. Describa una función
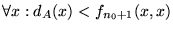 que sea efectivamente una BIYECCION.
que sea efectivamente una BIYECCION.
2. Códigos basados en primos: Consideremos a los primeros 7 números primos: 2, 3, 5, 7, 11, 13 y 17, y a la codificación de los elementos sintácticos de los programas-while 's
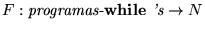 construída como sigue:
Representación de variables: A la variable Xw, donde
construída como sigue:
Representación de variables: A la variable Xw, donde
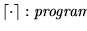 es una lista de 0's y 1's, la representamos por el número entero
es una lista de 0's y 1's, la representamos por el número entero
Codificación de instrucciones:
Codificación de programas:
a) Muestre que
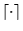 es una función inyectiva.
b) Describa a un procedimiento para calcular su inversa.
c) Decida si acaso es una biyección.
es una función inyectiva.
b) Describa a un procedimiento para calcular su inversa.
c) Decida si acaso es una biyección.
3. Considerando a la codificación con primos del ejercicio anterior, describa un procedimiento para calcular los códigos de los numerales.
4. Los códigos basados en primos crecen (excesivamente) rápido. Considerando a la biyección de Cantor describa una codificación similar a la basada en primos con un (mucho) menor crecimiento.
5. Muestre que la función
es recursiva primitiva.
6. Muestre que la función
es recursiva primitiva.
7. Muestre que la función
es recursiva primitiva.
Tenemos, por ejemplo, que para
 ,
,
8. Muestre que la función
es recursiva primitiva.
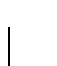 es la suma de divisores de x. Tenemos, por ejemplo, que para
es la suma de divisores de x. Tenemos, por ejemplo, que para
9. Muestre que la función
es recursiva primitiva.
10. Muestre que la función
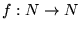 tal que
tal que
es recursiva primitiva.
11. Sea
Muestre que u es recursiva primitiva.
12. Muestre por doble inducción las propiedades siguientes:
a)
 .
b)
.
b)
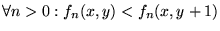 .
.
13. Muestre que
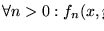 .
.
14. a) Describa un procedimiento para calcular la función exponenciación:
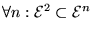 .
b) Describa un procedimiento más eficiente que el anterior para calcular a la exponenciación, o pruebe que el anterior no se puede mejorar.
Sugerencia: Para calcular x31 calcule la sucesión
.
b) Describa un procedimiento más eficiente que el anterior para calcular a la exponenciación, o pruebe que el anterior no se puede mejorar.
Sugerencia: Para calcular x31 calcule la sucesión
x, x2,x8,x16,x24,x28,x30,x31.
15. Un número real
![$x\in [0,1]$](img592.gif) es computable si la función
es computable si la función
es computable.
Muestre que todo número racional es computable.
16. Muestre que la raíz cuadrada de un número computable es computable.
17. Muestre mediante un argumento ``diagonal'' que existen números en el intervalo [0,1] que no son computables.
18. Muestre que 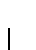 es computable.
Sugerencia: Puede utilizar cualquiera de las siguientes identidades:
es computable.
Sugerencia: Puede utilizar cualquiera de las siguientes identidades:
19. Sea
 una función de apareamiento y sean
una función de apareamiento y sean
sus correspondientes funciones proyecciones.
Sea
 la correspondiente enumeración de las sucesiones de naturales de longitud finita.
Muestre que las siguientes funciones
la correspondiente enumeración de las sucesiones de naturales de longitud finita.
Muestre que las siguientes funciones
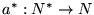 son computables:
son computables:
20. Muestre que las siguientes funciones
 son computables:
son computables:




Siguiente: Funciones de apareamiento y
Un nivel arriba: Funciones recursivas primitivas
Anterior: Función de Ackermann
Guillermo Morales-Luna
2000-07-10
![\begin{eqnarray*}{[\mbox{\it Inst};\mbox{\it Ruti}]} &\mapsto& 5^{\lceil\mbox{\i...
...{\mbox{\it Ruti}\}]} &\mapsto& 2^{\lceil\mbox{\it Ruti}\rceil}
\end{eqnarray*}](img574.gif)
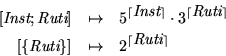
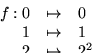
 ,
,
 es la suma de divisores de x. Tenemos, por ejemplo, que para
es la suma de divisores de x. Tenemos, por ejemplo, que para
 .
b)
.
b)
 una función de apareamiento y sean
una función de apareamiento y sean  la correspondiente enumeración de las sucesiones de naturales de longitud finita.
Muestre que las siguientes funciones
la correspondiente enumeración de las sucesiones de naturales de longitud finita.
Muestre que las siguientes funciones
 son computables:
son computables: