



Siguiente: Segunda lista de ejercicios
Un nivel arriba: Funciones recursivas primitivas
Anterior: Niveles de la jerarquía
Función de Ackermann
En la sección anterior presentamos una jerarquía para las funciones recursivas primitivas. Se vió que las funciones en un nivel de la jerarquía, que no se encuentran en el nivel anterior, tienen un crecimiento sustancialmente mayor que las funciones en el nivel anterior.
Extrapolaremos la construcción presentada para obtener una función con un crecimiento mayor que cualquier función en cualquier nivel de la jerarquía. Tal función no podrá ser recursiva primitiva, pero sí ha de ser computable. Veamos pues la construcción de esa función.
La función sucesor
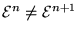 es muy sencilla, desde el punto de vista computacional.
La función suma es una reiteración de la sucesor:
es muy sencilla, desde el punto de vista computacional.
La función suma es una reiteración de la sucesor:
La función producto es una reiteración de la suma:
donde
La función exponencial es una reiteración del producto:
Continuando con estas reiteraciones podemos considerar
Esta es la motivación de la función de Ackermann.
Sea
 definida como sigue:
definida como sigue:
Para ilustrar el comportamiento de A, si escribimos
hn(m)=A(n,m) entonces tendremos
de lo cual resulta
donde
Se ve así que esta función crece extremadamente rápido.
Una manera de calcular la función de Ackermann es manipulando listas de índices. Utilizaremos ``corchetes'' para denotar aplicaciones sucesivas, siempre por la derecha, de la función de Ackermann. Precisamente,
Utilizaremos el símbolo ``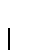 '' para denotar igualdad de listas bajo esta interpretación.
De la definición de la función tenemos
'' para denotar igualdad de listas bajo esta interpretación.
De la definición de la función tenemos
Así pues, dada una lista de enteros
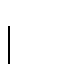 ,
separemos a sus dos últimos elementos, digamos
,
separemos a sus dos últimos elementos, digamos
L=L'*[n,m]
entonces calculamos la transformación
![\begin{displaymath}T(L)=\left\{\begin{array}{ll}
L'*{[}m+1{]} &\mbox{\rm si $n=...
...box{\rm si $n\not=0$\space y $m\not=0$ }.
\end{array}\right.
\end{displaymath}](img559.gif) |
(9) |
Tendremos el valor de A(n,m) al obtener, por primera vez, una lista de longitud 1 aplicando sucesivamente la transformación T, a partir de la lista [n,m].
En 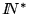 introduzcamos la relación ``
introduzcamos la relación ``
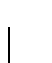 '' definiendo
'' definiendo
Resulta evidente que
-
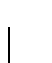 es una relación de orden,
es una relación de orden,
-
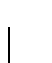 es un buen orden, es decir toda cadena posee un mínimo, si y sólo si el procedimiento descrito para calcular la función de Ackermann termina.
es un buen orden, es decir toda cadena posee un mínimo, si y sólo si el procedimiento descrito para calcular la función de Ackermann termina.
Un momento de reflexión basta para convencerse de que
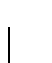 es, en efecto, un buen orden.
En la figura 2.1 se muestra un procedimiento alternativo para el cálculo de la función A. El seudocódigo ahí mostrado sigue una sintaxis à la FORTRAN.
es, en efecto, un buen orden.
En la figura 2.1 se muestra un procedimiento alternativo para el cálculo de la función A. El seudocódigo ahí mostrado sigue una sintaxis à la FORTRAN.
Figure 2.1:
Cálculo de la función de Ackermann.
|
|
Proposición 4.1
La función de Ackermann NO es recursiva primitiva.
Justificación: No entraremos en detalles. Tan solo diremos que debido a su definición, puede verse que la función
 domina, a la larga, a cada una de las funciones
domina, a la larga, a cada una de las funciones
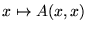 ,
es decir,
,
es decir,
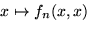 |
(10) |
Si A fuese recursiva primitiva, entonces su diagonal
 también sería recursiva primitiva, por lo cual existiría un índice n0 tal que
también sería recursiva primitiva, por lo cual existiría un índice n0 tal que
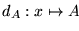 .
Por la proposición 2.3.7, se tiene
.
Por la proposición 2.3.7, se tiene
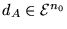 .
Esto contradice a la relación 2.10.
.
Esto contradice a la relación 2.10.




Siguiente: Segunda lista de ejercicios
Un nivel arriba: Funciones recursivas primitivas
Anterior: Niveles de la jerarquía
Guillermo Morales-Luna
2000-07-10
 definida como sigue:
definida como sigue:
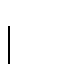 ,
separemos a sus dos últimos elementos, digamos
,
separemos a sus dos últimos elementos, digamos
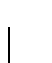 '' definiendo
'' definiendo
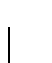 es una relación de orden,
es una relación de orden,
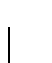 es un buen orden, es decir toda cadena posee un mínimo, si y sólo si el procedimiento descrito para calcular la función de Ackermann termina.
es un buen orden, es decir toda cadena posee un mínimo, si y sólo si el procedimiento descrito para calcular la función de Ackermann termina.
 es, en efecto, un buen orden.
En la figura 2.1 se muestra un procedimiento alternativo para el cálculo de la función A. El seudocódigo ahí mostrado sigue una sintaxis à la FORTRAN.
es, en efecto, un buen orden.
En la figura 2.1 se muestra un procedimiento alternativo para el cálculo de la función A. El seudocódigo ahí mostrado sigue una sintaxis à la FORTRAN.
 también sería recursiva primitiva, por lo cual existiría un índice n0 tal que
también sería recursiva primitiva, por lo cual existiría un índice n0 tal que