



Siguiente: Algoritmo de Euclides
Un nivel arriba: Función de Gödel
Anterior: Función de Gödel
Recordamos la relación de divisibilidad. Dados
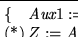 se dice que y divide a x, y se escribe x|y, si y sólo si
se dice que y divide a x, y se escribe x|y, si y sólo si
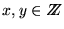 .
Es claro que esta relación es
.
Es claro que esta relación es
- Reflexiva
-
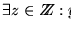 .
.
- Transitiva
-
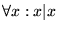 .
.
- Antisimétrica
- (Salvo unidades)
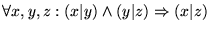
Consecuentemente, ``|'' es una relación de orden en el conjunto
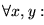 ,
que consta de los enteros estrictamente positivos. Es claro que los elementos minimales de este orden son los números primos.
,
que consta de los enteros estrictamente positivos. Es claro que los elementos minimales de este orden son los números primos.
Para cada
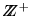 el conjunto de múltiplos de n es
el conjunto de múltiplos de n es
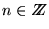 .
Resulta que
.
Resulta que 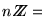 es un ideal de
es un ideal de 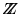 ,
es decir, se cumplen las propiedades siguientes:
,
es decir, se cumplen las propiedades siguientes:
Dados
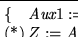 decimos que ellos son congruentes módulo n, y escribimos
decimos que ellos son congruentes módulo n, y escribimos 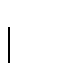 ,
si
,
si
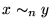 .
Resulta, ahora, que
.
Resulta, ahora, que 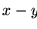 es una relación de equivalencia. El conjunto de clases de equivalencia, o cociente, es
es una relación de equivalencia. El conjunto de clases de equivalencia, o cociente, es
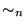 .
En consecuencia se tiene que
.
En consecuencia se tiene que
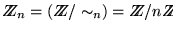 es un anillo, pues de hecho,
es un anillo, pues de hecho,
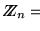 hereda la estructura de anillo de
hereda la estructura de anillo de 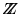 .
Si
.
Si 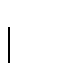 escribimos, como es más usual,
escribimos, como es más usual,
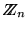 .
.
Dados dos enteros
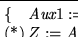 un máximo común divisor (m.c.d.) de la pareja x,y es un supremo del conjunto de cotas inferiores de
un máximo común divisor (m.c.d.) de la pareja x,y es un supremo del conjunto de cotas inferiores de 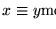 ,
respecto al orden de divisibilidad. Es decir, z es un m.c.d. de x,y si
,
respecto al orden de divisibilidad. Es decir, z es un m.c.d. de x,y si
En tal caso escribimos

Dados
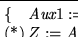 el ideal generado por x,y es el conjunto de combinaciones lineales de x e y; éste es
el ideal generado por x,y es el conjunto de combinaciones lineales de x e y; éste es
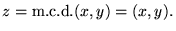
Si w es un divisor común de x e y entonces w es también un divisor de cualquier elemento en I(x,y).
Por tanto, el máximo común divisor (x,y) es el menor elemento positivo en el ideal generado por x,y. Así pues
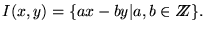 .
Además esa combinación en mínima.
.
Además esa combinación en mínima.




Siguiente: Algoritmo de Euclides
Un nivel arriba: Función de Gödel
Anterior: Función de Gödel
Guillermo Morales-Luna
2000-07-10
 ,
si
,
si
 escribimos, como es más usual,
escribimos, como es más usual,
