



Siguiente: Nociones de divisibilidad
Un nivel arriba: Funciones de apareamiento y
Anterior: Reiteración de funciones de
Esta función es una de las funciones de apareamiento más famosas en la historia de la lógica matemática. Kurt Gödel la utilizó para codificar fórmulas del cálculo de predicados por números. De esta forma pudo predicar sobre los mismos enunciados del cálculo de predicados. Tal propiedad de autoreferencia origina que, si se tuviese un sistema lógico consistente, codificable algorítmicamente en los número naturales, entonces el sistema ha de ser incompleto, vale decir, habrá enunciados que siendo universalmente válidos, no son demostrables. No es nuestro objeto estudiar aquí el teorema de incompletitud de Gödel y por tanto no abundaremos más sobre él. Sin embargo, tal tipo de argumentación lo hemos de utilizar en la presentación que hagamos de la noción de irresolubilidad.
La función 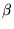 es muy sencilla desde el punto de vista de las funciones aritméticas y tiene un crecimiento moderado, comparado con otras funciones de apareamiento.
Comenzaremos presentando nociones básicas de la teoría de números, luego presentaremos el teorema chino del residuo, después haremos la construcción de la función
es muy sencilla desde el punto de vista de las funciones aritméticas y tiene un crecimiento moderado, comparado con otras funciones de apareamiento.
Comenzaremos presentando nociones básicas de la teoría de números, luego presentaremos el teorema chino del residuo, después haremos la construcción de la función 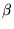 de Gödel y, finalmente, mencionaremos la manera en la que codifica secuencias de números.
de Gödel y, finalmente, mencionaremos la manera en la que codifica secuencias de números.




Siguiente: Nociones de divisibilidad
Un nivel arriba: Funciones de apareamiento y
Anterior: Reiteración de funciones de
Guillermo Morales-Luna
2000-07-10