



Siguiente: La noción de ``Universalidad''
Un nivel arriba: Universalidad
Anterior: Codificación de programas por
Numerabilidad de la clase de máquinas de Turing
En el primer capítulo vimos que las funciones computables también pueden presentarse como funciones computables por máquinas de Turing.
En este sección veremos que las máquinas de Turing conforman una clase efectivamente numerable e introduciremos en términos de ellas el concepto de universal.
Sin pérdida de generalidad supondremos de aquí en adelante que el alfabeto de las máquinas de Turing es
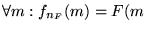 Al enumerar al conjunto de estados
Al enumerar al conjunto de estados
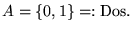 ,
cada pareja de la forma
,
cada pareja de la forma
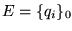 ,
donde p es un estado y t es un símbolo en S, se identifica con la cadena
,
donde p es un estado y t es un símbolo en S, se identifica con la cadena
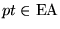 ,
donde i es el índice del estado p escrito en binario.
Recodifiquemos una cadena
,
donde i es el índice del estado p escrito en binario.
Recodifiquemos una cadena
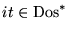 de símbolos 0,1 aplicando la sustitución
de símbolos 0,1 aplicando la sustitución
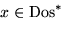 |
(13) |
y denotemos por c(x) al resultado de la sustitución.
Así por ejemplo
 .
Codifiquemos a los símbolos de movimiento mediante la correspondencia
.
Codifiquemos a los símbolos de movimiento mediante la correspondencia
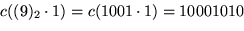 |
(14) |
En 3.3 y en 3.4 hemos codificado 5 símbolos ``originales![[*]](../images/spanish/icons.gif/foot_motif.gif) '', a saber
'', a saber
 ,
respectivamente por las cadenas 1k0,
k=0,1,2,3,4. Conforme surja la necesidad de aumentar símbolos originales, los codificaremos por cadenas 1k0 incrementando k según proceda.
Cada quíntupla de la forma qsptm queda codificada por la yuxtaposición de c(qspt), el código de m y de un separador de quíntuplas 150.
Una máquina de Turing
,
respectivamente por las cadenas 1k0,
k=0,1,2,3,4. Conforme surja la necesidad de aumentar símbolos originales, los codificaremos por cadenas 1k0 incrementando k según proceda.
Cada quíntupla de la forma qsptm queda codificada por la yuxtaposición de c(qspt), el código de m y de un separador de quíntuplas 150.
Una máquina de Turing
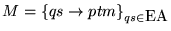 queda entonces codificada por la concatenación de los códigos de las quíntuplas qsptm que la describen, seguida de un separador de códigos de máquinas 160. Denotemos a este código por
queda entonces codificada por la concatenación de los códigos de las quíntuplas qsptm que la describen, seguida de un separador de códigos de máquinas 160. Denotemos a este código por
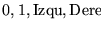 ,
el cual puede ser visto como la representación en binario de un número natural. Llamemos a este número el código de la máquina M.
La codificación que hemos bosquejado es algorítmicamente reversible:
Dado un número natural
,
el cual puede ser visto como la representación en binario de un número natural. Llamemos a este número el código de la máquina M.
La codificación que hemos bosquejado es algorítmicamente reversible:
Dado un número natural
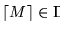 ,
,
- 1.
- lo escribimos en binario,
- 2.
- si aparecen más de seis 1's consecutivos el número no representa una máquina de Turing, le podemos asociar la máquina vacía,
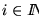 ,
i.e. la que no tiene quintupla alguna. En otro caso
,
i.e. la que no tiene quintupla alguna. En otro caso
- 3.
- decodificamos a las quíntuplas según el procedimiento inverso al arriba descrito. Si apareciese una inconsistencia, por ejemplo si apareciesen más quíntuplas que las necesarias, le asociamos la máquina vacía.
Tenemos así una enumeración
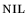 tal que para cualesquiera máquinas de Turing M1 y M2, que no sean
tal que para cualesquiera máquinas de Turing M1 y M2, que no sean
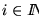 ,
se cumple la equivalencia lógica:
,
se cumple la equivalencia lógica:
El conjunto imagen de las máquinas de Turing no-vacías bajo la codificación que hemos construído, y que denotamos por
 NIL
NIL
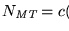 ,
consta de los códigos ``legales'' de máquinas de Turing.
Como un subconjunto de los números naturales,
,
consta de los códigos ``legales'' de máquinas de Turing.
Como un subconjunto de los números naturales,
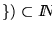 es numerable y, consecuentemente, la clase de máquinas de Turing también lo es. Sea
es numerable y, consecuentemente, la clase de máquinas de Turing también lo es. Sea
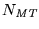 definido como
definido como
Entonces
 es una biyección
es una biyección
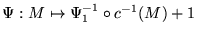 NIL
NIL
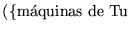 ,
la cual, haciendo
,
la cual, haciendo
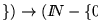 ,
se extiende a una enumeración de todas las máquinas de Turing. Si
,
se extiende a una enumeración de todas las máquinas de Turing. Si 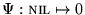 diremos que i es el índice de la máquina M y escribiremos M=Mi, así como también, redefiniendo operadores,
diremos que i es el índice de la máquina M y escribiremos M=Mi, así como también, redefiniendo operadores,
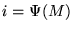 y
y
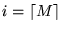 .
.




Siguiente: La noción de ``Universalidad''
Un nivel arriba: Universalidad
Anterior: Codificación de programas por
Guillermo Morales-Luna
2000-07-10
 .
Codifiquemos a los símbolos de movimiento mediante la correspondencia
.
Codifiquemos a los símbolos de movimiento mediante la correspondencia
 ,
respectivamente por las cadenas 1k0,
k=0,1,2,3,4. Conforme surja la necesidad de aumentar símbolos originales, los codificaremos por cadenas 1k0 incrementando k según proceda.
Cada quíntupla de la forma qsptm queda codificada por la yuxtaposición de c(qspt), el código de m y de un separador de quíntuplas 150.
Una máquina de Turing
,
respectivamente por las cadenas 1k0,
k=0,1,2,3,4. Conforme surja la necesidad de aumentar símbolos originales, los codificaremos por cadenas 1k0 incrementando k según proceda.
Cada quíntupla de la forma qsptm queda codificada por la yuxtaposición de c(qspt), el código de m y de un separador de quíntuplas 150.
Una máquina de Turing
 NIL
NIL