



Siguiente: Teoremas de recursión
Un nivel arriba: Virus en programas-while
Anterior: Definiciones básicas
Para mostrar que existen virus en el lenguaje de los programas-while necesitaremos arreglos planares infinitos, es decir, matrices cuyos renglones y columnas están siendo indicadas por los números naturales.
Una matriz infinita es un arreglo
![$M=\left[m_{ij}\right]_{i,j\geq 0}$](img939.gif) .
Denotemos a las matrices infinitas con entradas naturales y con entradas funciones recursivas, respectivamente, como
.
Denotemos a las matrices infinitas con entradas naturales y con entradas funciones recursivas, respectivamente, como
Sea
 una función y M una matriz. M se dice ser
una función y M una matriz. M se dice ser
- cerrada por renglones bajo la función f
- si
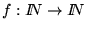 es decir, si para cada renglón en M, su imagen bajo la función f aparece también como otro renglón de la matriz M, y
es decir, si para cada renglón en M, su imagen bajo la función f aparece también como otro renglón de la matriz M, y
- diagonalmente completa
- si su diagonal aparece también como un renglón, es decir
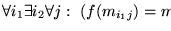
Lema 6.1 (Diagonal de punto fijo)
Si f es una función tal que existe una matriz diagonalmente completa cerrada por renglones bajo f entonces f posee un punto fijo, es decir, existe x tal que f(x)=x.
Demostración: Sea M una matriz diagonalmente completa cerrada por renglones bajo f. Sea id tal que
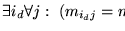 .
Existe ie tal que
.
Existe ie tal que
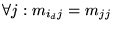 .
Para j=ie se tiene
f(midie)=m=midie.
Así pues
midie es un punto fijo de f.
.
Para j=ie se tiene
f(midie)=m=midie.
Así pues
midie es un punto fijo de f.




Siguiente: Teoremas de recursión
Un nivel arriba: Virus en programas-while
Anterior: Definiciones básicas
Guillermo Morales-Luna
2000-07-10
 una función y M una matriz. M se dice ser
una función y M una matriz. M se dice ser