Siguiente: Malas noticias: No hay Un nivel arriba: Virus en programas-while Anterior: Teoremas de recursión

Construcción de virus

Sea r el índice del programa Rep. Dado $x\in I\!\!N$ sea P_x un programa-while que hace lo siguiente:

1.

calcula $x_r=\mbox{\it Comp}(r,x)$, es decir, compone a Rep con el x-ésimo programa,

2.

deja a x_r como su valor final.

P_x es un programa que calcula un valor constante, x_r, que depende de x. Sea $g:I\!\!N\rightarrow I\!\!N,\ x\mapsto\mbox{\rm (\'\i ndice de }P_x)$. Evidentemente, $\forall x,y$: $f_{g(x)}(y)=\mbox{\it Comp}(r,x).$ La función g no tiene porqué ser extensional, sin embargo es computable. Por el Teorema de Recursión se tiene que $\exists n_0$ tal que f_n0=f_g(n0). Así pues, ambos f_n0 y f_g(n0) calculan a la función $y\mapsto \mbox{\it Comp}(r,n_0)$. Sea $P=\mbox{\it Rep}(\mbox{\it Comp}(r,n_0))$. Se ve fácilmente que P es un virus. Por un lado, tenemos que el índice de P es $\mbox{\it Comp}(r,n_0)$. Por otro lado, para todo y se ha de tener $P(y)= \mbox{\it Comp}(r,n_0).$

Observación 6.2   Las siguientes propiedades se siguen inmediatamente:

1.

Todo lenguaje de programación suficientemente capaz de contener un ``intérprete'' de él mismo (de programar las funciones Rep, Comp y Eval) es susceptible de ``engendrar'' virus.

2.

El virus se ``realiza'' como un punto fijo de una función de sustitución g. Esta es la base de los programas virus ``reales''.

3.

El procedimiento descrito en esta sección,

• es efectivo: en principio se puede escribir un programa que calcule a los índices r y k₀, así como también a los valores 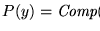$\mbox{\it Comp}(r,k_0)$ y $\mbox{\it Rep}(\mbox{\it Comp}(r,k_0))$,
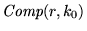• NO es eficiente: los cálculos anteriores son muy extensos y la sola enumeración de todos los programas es impráctica.

Siguiente: Malas noticias: No hay Un nivel arriba: Virus en programas-while Anterior: Teoremas de recursión