



Siguiente: Irresolubilidad
Un nivel arriba: Teoría de la recursividad
Anterior: Tercera lista de ejercicios
1. Aritmética de grandes números: Construir un módulo para el manejo de números enteros grandes (número de dígitos 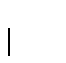 ). Represente números grandes como listas de enteros sin signos.
Construya la suma de enteros grandes procediendo según la intuición más elemental, llevando acarreos.
Construya el producto de enteros grandes procediendo según el algoritmo ``divide y vencerás'' del libro de Ullman: ``Design and analysis of algorithms''.
). Represente números grandes como listas de enteros sin signos.
Construya la suma de enteros grandes procediendo según la intuición más elemental, llevando acarreos.
Construya el producto de enteros grandes procediendo según el algoritmo ``divide y vencerás'' del libro de Ullman: ``Design and analysis of algorithms''.
2. Función de Ackerman: Implementar el cálculo, mediante ``pilas'' de la función de Ackerman A. Contar el número de accesos a la pila hechos durante el cálculo de A(m,n).
3. Función 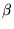 de Gödel: Implementar el cálculo de la función
de Gödel: Implementar el cálculo de la función 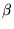 de Gödel. Graficarla en diferentes intervalos. Calcular su inversa mediante el Teorema Chino del residuo.
de Gödel. Graficarla en diferentes intervalos. Calcular su inversa mediante el Teorema Chino del residuo.
4. Minivirus en ``C'': Implementar los programas que se autorreproducen que aparecen en los paneles 5 y 7 del artículo de Witten: ``Computer (In)security: Infiltrating Open Systems'', ABACUS, Summer 1987, pp: 6-25.
5. Función de Ackerman: Implementar el cálculo, mediante el algoritmo cuyo seudocódigo se dió en la Nota 3 de la Parte I de las notas del curso, de la función de Ackerman A. Justificar su funcionamiento.
6. Códigos de Máquinas de Turing: Implementar la codificación de máquinas de Turing vistaen clase. Dada una máquina de Turing por su lista de quintuplas generar su código.
7. Máquina Universal de Turing: Generar una máquina universal de Turing según el método visto en clase.
8. Recopilación de un intérprete de programas-while 's: Recolectar los programas elaborados en los puntos 1.1-1.4,1.7 de esta lista y recopilarlos en un solo sistema que sea un intérprete de programas-while 's.




Siguiente: Irresolubilidad
Un nivel arriba: Teoría de la recursividad
Anterior: Tercera lista de ejercicios
Guillermo Morales-Luna
2000-07-10
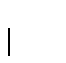 ). Represente números grandes como listas de enteros sin signos.
Construya la suma de enteros grandes procediendo según la intuición más elemental, llevando acarreos.
Construya el producto de enteros grandes procediendo según el algoritmo ``divide y vencerás'' del libro de Ullman: ``Design and analysis of algorithms''.
). Represente números grandes como listas de enteros sin signos.
Construya la suma de enteros grandes procediendo según la intuición más elemental, llevando acarreos.
Construya el producto de enteros grandes procediendo según el algoritmo ``divide y vencerás'' del libro de Ullman: ``Design and analysis of algorithms''.