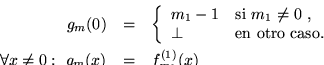Siguiente: Segunda lista de programas
Un nivel arriba: Teoría de la recursividad
Anterior: Malas noticias: No hay
En esta lista usaremos las notaciones siguientes
Dada una clase
 de funciones
de funciones
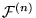 ,
una función universal para
,
una función universal para
 es una función
es una función
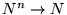 tal que
tal que
- Toda sección de U está en la clase
 ,
i.e.
,
i.e.
- Toda función en la clase se ``realiza'' como una sección de U:
En tal caso if es un índice de f correspondiente a U.
Sea
 una función de apareamiento, sea
una función de apareamiento, sea
 una clase de funciones
una clase de funciones
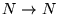 y sea
y sea
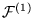 una función universal para
una función universal para
 .
Diremos que
.
Diremos que
 contiene a su propia función universal si
contiene a su propia función universal si
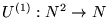 .
.
1. Resuelva la ecuación
2. Resuelva el sistema de ecuaciones
3. Resuelva el sistema de ecuaciones
4. Construya una función universal para los polinomios de una sola variable con coeficientes en Z, i.e. para la clase Z[x].
5. Muestre que toda familia finita de funciones posee una función universal.
6. Diremos que una función
 es general si para cualquier
es general si para cualquier 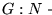 existe una función computable total
existe una función computable total
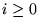 tal que
tal que
a) Muestre que existen funciones generales.
Sugerencia: Considere una función universal U(1), la enumeración de Cantor c y sus respectivas proyecciones
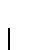 y
y
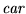 .
Considere
.
Considere
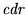 .
b) Muestre que existen funciones que no son generales.
c) Muestre que existe una infinidad de funciones generales.
.
b) Muestre que existen funciones que no son generales.
c) Muestre que existe una infinidad de funciones generales.
7. Sea
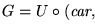 la enumeración de Cantor y sea
la enumeración de Cantor y sea
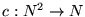 su k-ésima iteración:
su k-ésima iteración:
a) Bosqueje la construcción de un programa-while que calcule c. Sea m el número de variables en este programa.
b) Bosqueje la construcción de un programa-while que calcule ck utilizando a lo sumo m+k variables.
8. Muestre que la clase de funciones recursivas
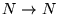 contiene a su propia función universal.
contiene a su propia función universal.
9. Sea 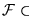 la mínima clase de funciones
la mínima clase de funciones
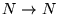 que contiene a la función cero y a la diagonal
que contiene a la función cero y a la diagonal
 ,
donde a es una función (computable) de apareamiento, y que es cerrada bajo el esquema de composición de funciones.
Muestre que
,
donde a es una función (computable) de apareamiento, y que es cerrada bajo el esquema de composición de funciones.
Muestre que 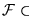 no puede contener a ninguna función universal suya.
Sugerencia: Revise el Lema de la Diagonal.
no puede contener a ninguna función universal suya.
Sugerencia: Revise el Lema de la Diagonal.
10. Muestre que Z[x] no puede contener a ninguna función universal suya.
11. Sea
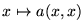 la función
la función
Muestre que F no puede ser recursiva.
12. Sea
 la función
la función
Muestre que 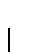 sí es recursiva.
sí es recursiva.
13. Decida si acaso la función
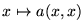 tal que
tal que
es recursiva. Justifique su respuesta.
14. Muestre que la función
es computable.
Sugerencia: Dado (i,j) ``simule'' la corrida en paralelo de los cálculos de los valores
 ,
parándose con el valor requerido cuando se pare el primero, en pararse, de esos cálculos.
,
parándose con el valor requerido cuando se pare el primero, en pararse, de esos cálculos.
15. Muestre que la función
es computable.
Sugerencia: Proceda como en el ejercicio anterior recorriendo, digamos que mediante la enumeración de Cantor, a los elementos
con k>j , 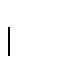 .
.
16. Sean
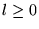 dos funciones computables. Construya una función computable
dos funciones computables. Construya una función computable
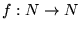 que satisfaga las siguientes dos condiciones
que satisfaga las siguientes dos condiciones
17. Muestre que la función
es computable.
18. Definiremos una nueva enumeración
de las funciones recursivas
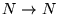 como sigue:
Sea
como sigue:
Sea
 una función computable de apareamiento con proyecciones respectivas
una función computable de apareamiento con proyecciones respectivas
 .
Dado
.
Dado 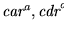 ,
escribamos
,
escribamos
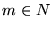 y
y
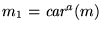 .
Entonces
.
Entonces
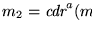 es la función definida por las siguientes dos relaciones:
es la función definida por las siguientes dos relaciones:
Muestre que la enumeración anterior es biyectiva, es decir
19. Considere la enumeración  del ejercicio anterior. Muestre que existe una función recursiva H tal que
del ejercicio anterior. Muestre que existe una función recursiva H tal que
20. Decida si acaso existe una función recursiva G ``inversa'' de la anterior, es decir, tal que




Siguiente: Segunda lista de programas
Un nivel arriba: Teoría de la recursividad
Anterior: Malas noticias: No hay
Guillermo Morales-Luna
2000-07-10
![\begin{eqnarray*}\left\{f_i\right\}_{i\geq 0} &:&\mbox{\rm\begin{minipage}[t]{25...
...funciones recursivas cuyo dominio es $N^n$ .\end{minipage}} \\
\end{eqnarray*}](img979.gif)
![\begin{eqnarray*}\left\{f_i\right\}_{i\geq 0} &:&\mbox{\rm\begin{minipage}[t]{25...
...funciones recursivas cuyo dominio es $N^n$ .\end{minipage}} \\
\end{eqnarray*}](img979.gif)
 de funciones
de funciones
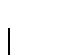 es una función
es una función
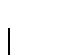 ,
i.e.
,
i.e.
 una función de apareamiento, sea
una función de apareamiento, sea
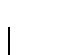 una clase de funciones
una clase de funciones
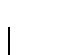 .
Diremos que
.
Diremos que
 contiene a su propia función universal si
contiene a su propia función universal si
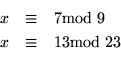
 es general si para cualquier
es general si para cualquier  ,
donde a es una función (computable) de apareamiento, y que es cerrada bajo el esquema de composición de funciones.
Muestre que
,
donde a es una función (computable) de apareamiento, y que es cerrada bajo el esquema de composición de funciones.
Muestre que  la función
la función
 ,
parándose con el valor requerido cuando se pare el primero, en pararse, de esos cálculos.
,
parándose con el valor requerido cuando se pare el primero, en pararse, de esos cálculos.
 .
.
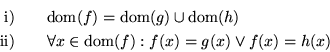
 una función computable de apareamiento con proyecciones respectivas
una función computable de apareamiento con proyecciones respectivas
 .
Dado
.
Dado