



Siguiente: Irresolubilidad de problemas en
Un nivel arriba: Problema de la correspondencia
Anterior: Presentación del Problema de
Veremos aquí un problema típico relativo a gramáticas libres de contexto que es irresoluble, y cuya irresolubilidad se demuestra viendo que es equivalente al Problema de la Correspondencia de Post.
Recordamos las siguientes definiciones
- Una palabra w en el lenguaje libre de contexto (LLC) L es ambigua en una GLC G que genere a L si w posee más de una derivación siniestra (leftmost) en G.
Como un ejemplo trivial, se tiene que, en la gramática con producciones
 ,
,
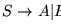 ,
,
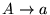 ,
la palabra a posee dos derivaciones siniestras
,
la palabra a posee dos derivaciones siniestras
- Una GLC G es ambigua si hay una palabra, del lenguaje que genera, ambigua en ella.
- Un LLC L es inherentemente ambiguo si cualquier GLC G que lo genere es ambigua.
A guisa de ejemplo se tiene que el lenguaje
es inherentemente ambiguo.
Sin que presentemos aquí una demostración formal de esta aseveración, daremos una motivaci''on intuitiva de ella. Seguramente el lector no tendrá ninguna dificultad en visualizar una GLC para generar L1 y otra para generar L2. Ahora, consideremos el lenguaje
 Tenemos que
Tenemos que
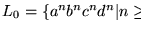 y cada palabra en L0 puede ser derivada tanto por la gramaática de L1 como por la gramaática de L2. Una y otra derivación hacen que cada papalabra de L0 se a ambigua (para cualquier gramática de L).
y cada palabra en L0 puede ser derivada tanto por la gramaática de L1 como por la gramaática de L2. Una y otra derivación hacen que cada papalabra de L0 se a ambigua (para cualquier gramática de L).
El Problema de Reconocimiento de Ambigüedad en GLC (PRAGLC) es el siguiente:
Instancia:
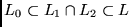
Solución:
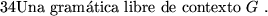
Proposición 2.2
PCP se reduce algorítmicamente a PRAGLC. Por tanto este último es irresoluble.
Demostración: Dada una instancia
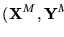 de PCP hemos de construir una instancia
de PCP hemos de construir una instancia
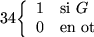 de PRAGLC, la cual consistirá de una gramática
de PRAGLC, la cual consistirá de una gramática
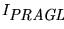 ,
de manera que
,
de manera que
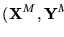 posea solución en PCP si y sólo si
posea solución en PCP si y sólo si
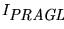 sea ambigua.
Denotemos por A al alfabeto de PCP. Escribamos
sea ambigua.
Denotemos por A al alfabeto de PCP. Escribamos
![$\mbox{\bf X} =\left[\mbox{\bf x}_1\cdots \mbox{\bf x}_k\right]$](img1134.gif) ,
,
![$\mbox{\bf Y}=\left[\mbox{\bf y}_1\cdots \mbox{\bf y}_k\right]$](img1135.gif) ,
y extendamos A incluyendo k nuevos símbolos
,
y extendamos A incluyendo k nuevos símbolos
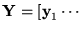 .
Construyamos los siguientes dos lenguajes:
.
Construyamos los siguientes dos lenguajes:
Sea
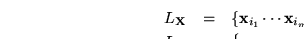 la GLC cuyas producciones son:
la GLC cuyas producciones son:
Resultan evidentes las propiedades siguientes:
- El lenguaje generado por esta gramática es

-
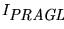 es ambigua si y sólo si se cumple cualquiera de las siguientes dos proposiciones claramente equivalentes entre sí:
es ambigua si y sólo si se cumple cualquiera de las siguientes dos proposiciones claramente equivalentes entre sí:
- 1.
-
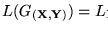
- 2.
-
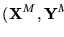 posee solución en PCP.
posee solución en PCP.




Siguiente: Irresolubilidad de problemas en
Un nivel arriba: Problema de la correspondencia
Anterior: Presentación del Problema de
Guillermo Morales-Luna
2000-07-10
 ,
,
