



Siguiente: Una aplicación de PCP
Un nivel arriba: Problema de la correspondencia
Anterior: Problema de la correspondencia
Sea A un alfabeto finito y sea A* su diccionario. El problema de la correspondencia de Post (PCP) se define como sigue:
Instancia:
![\begin{pagi}{34}Dos listas $\mbox{\bf X}=\left[\mbox{\bf x}_i\right]_{i=1,\ldots...
...con un mismo n\'umero de elementos, formadas por palabras en $A^*$ .
\end{pagi}](img1071.gif)
Solución:
![\begin{pagi}{34}Una lista de \'\i ndices $\mbox{\bf I}\in \{1,\ldots,n\}^{\mbox{...
..._{i_m}]=[\mbox{\bf y}_{i_1}\cdots\mbox{\bf y}_{i_m}].\end{displaymath}\end{pagi}](img1072.gif)
Ejemplos
Consideremos
Para
![$\mbox{\bf I}=[5,2,3,3,6]$](img1074.gif) se tiene
se tiene
pues
En cambio para
el PCP no tiene solución alguna. (¡Revísese!)
El problema de la correspondencia de Post modificado (PCPM) coincide con el anterior salvo en que en este último se impone la exigencia de que la cadena común formada comience con las primeras palabras en las listas dadas:
Instancia:
![\begin{pagi}{34}Dos listas $\mbox{\bf X}=\left[\mbox{\bf x}_i\right]_{i=1,\ldots...
...con un mismo n\'umero de elementos, formadas por palabras en $A^*$ .
\end{pagi}](img1071.gif)
Solución:
![\begin{pagi}{34}Una lista de \'\i ndices $\mbox{\bf I}\in \{1,\ldots,n\}^{\mbox{...
...bf y}_{1}\mbox{\bf y}_{i_1}\cdots\mbox{\bf y}_{i_m}].\end{displaymath}\end{pagi}](img1078.gif)
Proposición 2.1
Si PCP fuera efectivamente resoluble entonces PCPM lo sería también.
Demostración: Traduciremos toda instancia
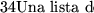 de PCPM, con n palabras en cada lista, a una instancia
de PCPM, con n palabras en cada lista, a una instancia
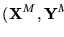 de PCP de manera que la instancia traducida posea una solución cuando y sólo cuando la instancia original también posea una correspondiente solución. Al traducir utilizaremos dos nuevos símbolos separadores ``
de PCP de manera que la instancia traducida posea una solución cuando y sólo cuando la instancia original también posea una correspondiente solución. Al traducir utilizaremos dos nuevos símbolos separadores ``
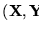 ''.
Ilustraremos el procedimiento con el ejemplo anterior con solución
''.
Ilustraremos el procedimiento con el ejemplo anterior con solución
![$\mbox{\bf I}=[5,2,3,3,6]$](img1074.gif) .
Para partir de una solución de PCPM, intercambiaremos las palabras primera y quinta en cada conjunto de palabras:
.
Para partir de una solución de PCPM, intercambiaremos las palabras primera y quinta en cada conjunto de palabras:
La solución es pues
![$\mbox{\bf I}=[1,2,3,3,6]$](img1083.gif) .
Para hacer la conversión, cambiaremos primero a las listas de palabras
.
Para hacer la conversión, cambiaremos primero a las listas de palabras
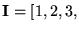 ,
después introduciremos nuevas palabras iniciales y nuevas palabras terminales.
Veamos ahora cómo corresponden soluciones de PCPM a soluciones de PCP y viceversa.
,
después introduciremos nuevas palabras iniciales y nuevas palabras terminales.
Veamos ahora cómo corresponden soluciones de PCPM a soluciones de PCP y viceversa.
Teorema 2.1
PCP es irresoluble.
Demostración: Veremos que PCPM no puede resolverse efectivamente. Para esto veremos cómo una instancia del Problema de la Parada en máquinas de Turing (PPmT) se reduce algorítmicamente a una instancia de PCPM de manera que la instancia a reducirse ha de poseer una solución, es decir, se reconocerá que la máquina ``instancia'' se parará a partir del contenido inicial ``instancia'', en PPmT si y sólo si la correspondiente instancia ya reducida posee una solución para PCPM. Siendo entonces PPmT reducible a PCPM se sigue inmediatamente que este último problema no puede ser resoluble pues si lo fuera, PCmT también lo sería, lo cual es imposible.
Sea pues
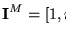 una instancia de PPmT: M es una mT y
una instancia de PPmT: M es una mT y
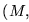 es una entrada para M. Sea
es una entrada para M. Sea
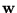 el alfabeto consistente de los símbolos y los estados de M, y de un símbolo para indicar extremos de DI's. Construiremos dos sucesiones de palabras
el alfabeto consistente de los símbolos y los estados de M, y de un símbolo para indicar extremos de DI's. Construiremos dos sucesiones de palabras
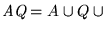 tales que
tales que
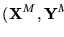 posee solución en PCP si y sólo si
posee solución en PCP si y sólo si
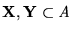 y en tal caso una solución de PCPM ha de consistir, propiamente, de una computación terminal que transforma la DI inicial
y en tal caso una solución de PCPM ha de consistir, propiamente, de una computación terminal que transforma la DI inicial
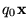 en alguna DI final.
Las construcciones de ambas listas
en alguna DI final.
Las construcciones de ambas listas
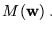 se hacen por etapas. En las tablas 5.1-5.3 quedan mostradas las palabras formadas para sendas listas
se hacen por etapas. En las tablas 5.1-5.3 quedan mostradas las palabras formadas para sendas listas
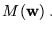 divididas por grupos: en el primer grupo presentamos partículas iniciales y las relativas al alfabeto de la m.T., en el segundo grupo aparecen las que codifican el funcionamiento de la m.T. y en el tercer grupo se enlista a las partículas terminales.
divididas por grupos: en el primer grupo presentamos partículas iniciales y las relativas al alfabeto de la m.T., en el segundo grupo aparecen las que codifican el funcionamiento de la m.T. y en el tercer grupo se enlista a las partículas terminales.
Table 5.1:
Grupo I: Parejas iniciales y de símbolos en la m. T.
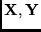 |
Table 5.2:
Grupo II: Parejas de transiciones.
 |
Table 5.3:
Grupo III: Parejas de estados finales y DI's terminales.
 |
Veamos que una solución de PPmT da una solución para PCPM.
Se dice que una pareja
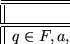 es una solución parcial de PCPM si
es una solución parcial de PCPM si
- C es un prefijo de D, y
- C y D son yuxtaposiciones de correspondientes cadenas en las listas
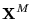 y
y
 ,
es decir, si
,
es decir, si
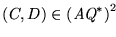 entonces
entonces
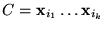 ,
donde
,
donde
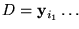 .
En tal caso, la partícula E es el residuo de la solución parcial (C,D).
.
En tal caso, la partícula E es el residuo de la solución parcial (C,D).
Se ve que las siguientes dos proposiciones son equivalentes:
- 1.
- La sucesión de DI's
 es una computación, intermedia o terminal, de longitud k+1 en la m. T. M, es decir
es una computación, intermedia o terminal, de longitud k+1 en la m. T. M, es decir
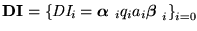 .
.
- 2.
- Si
entonces (Ck,Dk) es una solución parcial de PCPM.
Las dos implicaciones a demostrar se prueban por inducción en k.
Ahora, con la notación anterior, observamos que la solución parcial de la forma (Ck,Dk) más pequeña corresponde a cuando Ek es la palabra vacía. También observamos que si no aparecen palabras del grupo III, entonces en toda solución parcial (Ck,Dk), la longitud de Dk es estrictamente mayor que la de Ck. Por tanto, se tendrá una solución a PCPM si y sólo si se tiene una computación terminal en la máquina dada.




Siguiente: Una aplicación de PCP
Un nivel arriba: Problema de la correspondencia
Anterior: Problema de la correspondencia
Guillermo Morales-Luna
2000-07-10
![\begin{displaymath}\begin{array}{lcl}
\mbox{\bf X}={\left[\begin{array}{l}
\mb...
...11 \\ 0 \\ 1 \\ 1110 \\ 11101 \end{array}\right]}
\end{array}\end{displaymath}](img1073.gif)
![\begin{displaymath}\begin{array}{lcl}
\mbox{\bf X}={\left[\begin{array}{l}
\mb...
...11 \\ 0 \\ 1 \\ 1110 \\ 11101 \end{array}\right]}
\end{array}\end{displaymath}](img1073.gif)
![$\mbox{\bf I}=[5,2,3,3,6]$](img1074.gif) se tiene
se tiene
![$\mbox{\bf I}=[5,2,3,3,6]$](img1074.gif) .
Para partir de una solución de PCPM, intercambiaremos las palabras primera y quinta en cada conjunto de palabras:
.
Para partir de una solución de PCPM, intercambiaremos las palabras primera y quinta en cada conjunto de palabras:
![$\mbox{\bf I}=[1,2,3,3,6]$](img1083.gif) .
Para hacer la conversión, cambiaremos primero a las listas de palabras
.
Para hacer la conversión, cambiaremos primero a las listas de palabras
 e
e
 e
e
![$\mbox{\bf I}^M=[1,i_1,\ldots,i_k]$](img1099.gif) es una solución de PCPM entonces
es una solución de PCPM entonces