Siguiente: Semánticas basadas en conjunción Un nivel arriba: Lógicas proposicionales difusas Anterior: Sintaxis

Semánticas basadas en conjunción y negación

A toda forma proposicional se le puede asociar un valor de verdad, el cual ha de estar en función de los valores de verdad de las variables proposicionales que aparezcan en la forma proposicional y de la estructura de esa forma.

Una asignación es una función $v:P\rightarrow [0,1]$ que a cada variable proposicional $p\in P$ le asocia un valor de verdad $v(p)\in [0,1]$. Si v(p)=1 decimos que p es verdadera, en tanto que si v(p)=0 decimos que p es falsa. A toda asignación v la podemos extender a las constantes 0, 1 haciendo p(0)=0 y p(1)=1.

Como un primer enfoque para asociar valores de verdad a todas las formas proposicionales, sea $N:[0,1]\rightarrow[0,1]$ una negación y sea $\diamond:[0,1]^2\rightarrow[0,1]$ un operador conjuntor. Entonces, a toda asignación $v:P\rightarrow [0,1]$ se le puede extender a una función $v^*:\mbox{\it FP}\rightarrow[0,1]$ de manera inductiva:

$$\begin{eqnarray*}\forall p\in P:\hspace{2cm} v^*(p) &=& v(p) \\ v^*(\neg \phi)... ...2)))\diamond \\ &\ & N(N(N(v^*(\phi_2)))\diamond N(v^*(\phi_1))) \end{eqnarray*}$$

En adelante confundiremos a v^* con v. Veamos algunos ejemplos.

Min-Max.

Sea $x\diamond y=\mathop{\rm Min}\{x,y\}$ y N(x)=N₁(x)=1-x. Entonces,

$$\begin{eqnarray*}v(\neg_{\mbox{\scriptsize\it MM}}\phi) &=& 1-v(\phi) \\ v(\phi... ...phi_1),v(\phi_2)\},\mathop{\rm Max}\{1-v(\phi_2),v(\phi_1)\}\} % \end{eqnarray*}$$

Las gráficas de estas funciones coinciden con las mostradas en la figura 13.

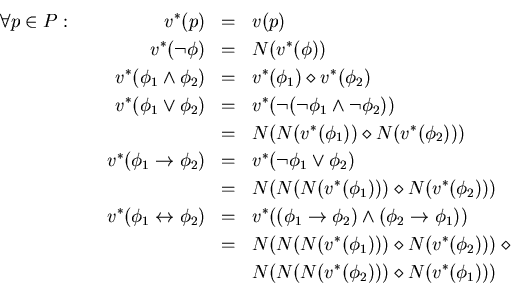
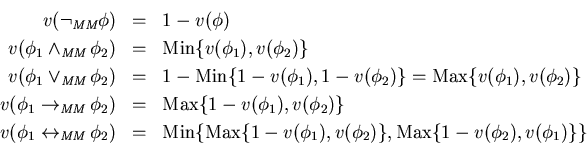
Por ejemplo, consideremos las proposiciones que formalizan el acertijo al final de la subsección anterior. Escribamos a=v(p_A), b=v(p_B) y c=v(p_C). Entonces, en la interpretación Min-Max se tiene:

$$\begin{eqnarray*}v(p_A\land \neg p_b \rightarrow p_C) &=& \mathop{\rm Max}[1-\ma... ...-a,1-c] \\ v(p_A\lor p_B\lor p_C) &=& \mathop{\rm Max}[a,b,c] % \end{eqnarray*}$$

Así pues, para cualquier valor $k\in[0,1]$ se tiene que cada una de estas proposiciones tiene un valor mayor o igual a k si y sólo si $k\leq \mathop{\rm Min}[(1-a),b]$ o bien $k\leq \mathop{\rm Min}[(1-c),b]$. En otras palabras, los cuatro hechos serán tanto más verdaderos cuanto a la vez A es inocente y B es culpable, o bien C es inocente y B es culpable (en cualquiera de los dos casos, la culpabilidad o inocencia del tercer sospechoso es irrelevante).

Producto-D.

Sea $x\diamond y=xy$y N(x)=N₁(x)=1-x. Entonces,

$$\begin{eqnarray*}v(\neg_{\mbox{\scriptsize\it PrD}}\phi) &=& 1-v(\phi) \\ v(\ph... ...-v(\phi_1)+v(\phi_1)v(\phi_2))(1-v(\phi_2)+v(\phi_1)v(\phi_2)) % \end{eqnarray*}$$

Las gráficas de estas funciones coinciden con las mostradas en la figura 14.

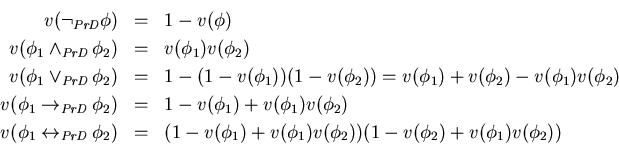
Con el mismo ejemplo del acertijo, en la interpretación Producto-D, se tiene:

$$\begin{eqnarray*}v(p_A\land \neg p_b \rightarrow p_C) &=& 1 - a + a b + a c - a ... ...a + b - a b + c - a c - b c + a b c \\ &=& 1-(1-a)(1-b)(1-c) % \end{eqnarray*}$$

Así pues, para cualquier $k\in[0,1]$, cada una de estas proposiciones tiene un valor mayor o igual a k si y sólo si se cumplen las siguientes cuatro desigualdades:

$$\begin{eqnarray*}a (1-b)(1-c) &\leq& 1 - k \\ (1-a)(1-b) c &\leq& 1 - k \\ a c &\leq& 1 - k \\ (1-a)(1-b)(1-c) &\leq& 1 - k \end{eqnarray*}$$

Por ejemplo, si a y (1-b) son pequeñas (independientemente del valor de c), es decir Aes inocente y B culpable, entonces k tiende a ser 1, es decir, los hechos tienden a ser verdaderos, y el recíproco también vale. Lo mismo pasa si c y (1-b) son pequeños. En suma, al igual que antes se vió, bien A es inocente y B culpable, o bien C es inocente y B culpable.

ukasiewicz-D.

Sea $x\diamond y=\mathop{\rm Max}\{x+y-1,0\}$ y N(x)=N₁(x)=1-x. Entonces,

$$\begin{eqnarray*}v(\neg_{\mbox{\scriptsize\it\L D}}\phi) &=& 1-v(\phi) \\ v(\ph... ...) &\mbox{ si $v(\phi_1)\leq v(\phi_2)$ . } \end{array}\right. % \end{eqnarray*}$$

Las gráficas de estas funciones coinciden con las mostradas en la figura 15.

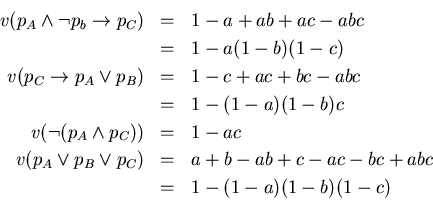
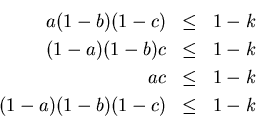
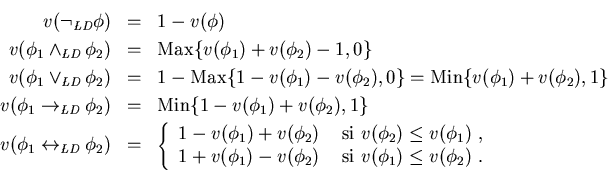
Siguiendo con el ejemplo del acertijo, en la interpretación ukasiewicz-D, se tiene:

$$\begin{eqnarray*}v(p_A\land \neg p_b \rightarrow p_C) &=& \mathop{\rm Min}[1, 1 ... ..., } \\ a+b+c &\mbox{ si $a+b+c\leq 1$ . } \end{array}\right. % \end{eqnarray*}$$

Así pues, para cualquier $k\in[0,1]$, cada una de estas proposiciones tiene un valor mayor o igual a k si y sólo si ocurre bien que $a<b\&a+b\geq k$ o bien $c<b\& c+b\geq k$

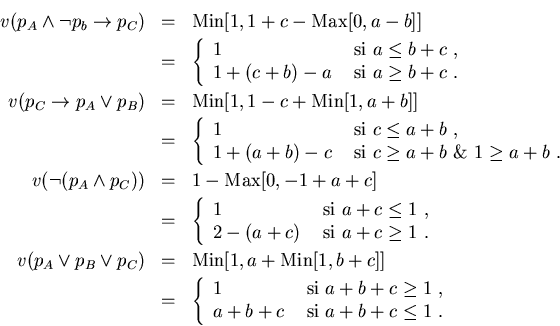
En todo cálculo proposicional difuso surgen entonces dos problemas:

Problema 3.1 (Propagación de incertidumbres hacia adelante)   Dada una asignación $v:P\rightarrow [0,1]$ y una forma proposicional $\phi(p_1,\ldots,p_n)$ determinar el valor $v\left(\phi\left(p_1,\ldots,p_n\right)\right)$ que ha de asumir $\phi$bajo la asignación v.

Problema 3.2 (Propagación de incertidumbres hacia atrás)   Dada una asignación $v:P\rightarrow [0,1]$ y m formas proposicionales con sus respectivos valores asumidos bajo la asignación v, $V_1=v\left(\phi_1\left(p_1,\ldots,p_n\right)\right), \ldots, V_m=v\left(\phi_m\left(p_1,\ldots,p_n\right)\right)$, determinar los valores $v(p_1),\ldots,v(p_n)$ que han de haber asumido las variables proposicionales bajo la asignación v.

La propagación de incertidumbres hacia adelante se restringe, en el caso del cálculo proposicional clásico a la evaluación de tablas de verdad. Prácticamente, las solas definiciones de los, así llamados, operadores veritativos correspondientes a los conectivos proporcionan algoritmos para resolver este problema. Una medida de la dificultad en resolverlo es el número de conectivos que aparecen en la forma proposicional dada: El problema será tanto más tardado cuánto más conectivos aparezcan en la fórmula dada.

El segundo problema, la propagación de incertidumbres hacia atrás, suele decirse, también, de diagnóstico: Si se tiene síntomas con una cierta intensidad, y éstos pueden depender de alguna manera de causas ``atómicas'' distinguidas, entonces ¿en qué medida están presentes esas causas para ocasionar tales síntomas?

Existen diversos tratamientos para estos problemas, los cuales dependen, primeramente, de los operadores veritativos involucrados, y en un segundo plano, de la sintaxis de las formas proposicionales dadas. Los métodos de demostración automática de teoremas resuelven (aún cuando parcialmente) este problema. Remitimos pues al lector a los capítulos en el presente volumen relativos a demostración automática y a programación lógica para conocer algunos de estos métodos. La explotación práctica de esas técnicas ha dado origen a los ``sistemas expertos''. En la literatura técnica (p. ej. [1,8]) se puede encontrar mucha información sobre este tema.

Siguiente: Semánticas basadas en conjunción Un nivel arriba: Lógicas proposicionales difusas Anterior: Sintaxis