Siguiente: Semánticas basadas en implicación Un nivel arriba: Lógicas proposicionales difusas Anterior: Semánticas basadas en conjunción

Semánticas basadas en conjunción e implicación

Como una observación complementaria a la Observación 2.3 tenemos que el conjunto de operadores $\{\cap,\mbox{\it .imp.}\}$ es también completo.

En efecto, el complemento puede obtenerse haciendo $\overline{A}=(A\mbox{\it .imp.} \emptyset)$. Así que, alternativamente, si se define un operador correspondiente a $\mbox{\it .imp.}$, junto con un conjuntor, se puede definir operadores correspondientes a los demás conectivos.

Sea pues $\diamond:[0,1]^2\rightarrow[0,1]$ un operador conjuntor. Definamos $\mbox{\it Imp}:[0,1]^2\rightarrow[0,1]$ como $\mbox{\it Imp}(x,y)=\mathop{\rm Max}\{z\in[0,1]\vert z\diamond x\leq y\}$. Es decir,

$$\forall z\in[0,1]:\ \ z\leq\mbox{\it Imp}(x,y)\ \Leftrightarrow\ z\diamond x\leq y.$$ (6)

$\mbox{\it Imp}$ se dice ser el residuo del operador conjuntor $\diamond$.

Los valores de verdad de los conectivos podrían ser, en una primera instancia, los siguientes:

  

$$v(\neg \phi) \mbox{\it Imp}(v(\phi),0)$$ = (7)

$$v(\phi_1\land \phi_2) v(\phi_1)\diamond v(\phi_2)$$ =

$$v(\phi_1\lor \phi_2) \mbox{\it Imp}(\mbox{\it Imp}(v(\phi_1),0),v(\phi_2))$$ = (8)

$$v(\phi_1\rightarrow \phi_2) \mbox{\it Imp}(v(\phi_1),v(\phi_2))$$ =

$$v(\phi_1\leftrightarrow \phi_2) \mbox{\it Imp}(v(\phi_1),v(\phi_2))\diamond \mbox{\it Imp}(v(\phi_2),v(\phi_1))$$ =

Sin embargo estas últimas definiciones son inadecuadas pues harían que la disyunción no fuera conmutativa. Para ver que, en efecto, esto ocurre, formulemos primeramente la siguiente:

Observación 3.1   Sea $\diamond:[0,1]^2\rightarrow[0,1]$ un operador conjuntor tal que ``no tenga divisores de cero'', es decir,

$$\forall x,y\in[0,1]:\ \ (x\not=0)\&(y\not=0)\ \Rightarrow\ x\diamond y\not=0.$$ (9)

Sea $\mbox{\it Imp}:[0,1]^2\rightarrow[0,1]$ definida como en la ecuación (6) arriba. Entonces:

1.

$\forall x,y\in[0,1]:\ \ (x>y)\ \Rightarrow\ \mbox{\it Imp}(x,y)<1$.

2.

$\forall x,y\in[0,1]:\ \ (x\leq y)\ \Rightarrow\ \mbox{\it Imp}(x,y)=1$.

3.

$\forall y\in[0,1]:\ \ \mbox{\it Imp}(0,y)=1$.

4.

$\forall x\in[0,1]:\ \ (x\not= 0)\ \Rightarrow\ \mbox{\it Imp}(x,0)=0$.

5.

$\forall y\in[0,1]:\ \ \mbox{\it Imp}(1,y)=y$.

6.

$\forall x\in[0,1]:\ \ \mbox{\it Imp}(x,1)=1$.

Consecuentemente, la negación $x\mapsto\mbox{\it Imp}(x,0)$, definida como en la ecuación (7) arriba, coincide con $N_{\infty}: x\mapsto \left\{\begin{array}{ll} 1 &\mbox{ si $x=0$ , } \\ 0 &\mbox{ si $x>0$ . } \end{array}\right.$

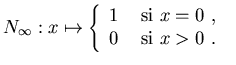
Omitiremos la demostración y nos permitimos encargársela al lector como un ejercicio.

Así pues, de acuerdo con la ecuación (8) arriba:

$$\begin{eqnarray*}v(\phi_1)=0 &\Rightarrow& \mbox{\it Imp}(v(\phi_1),0)=1 \\ &\... ...ghtarrow& v(\phi_1\lor \phi_2) = \mbox{\it Imp}(0,v(\phi_2)) = 1 \end{eqnarray*}$$

es decir, $v(\phi_1\lor \phi_2) = \left\{\begin{array}{ll} v(\phi_2) &\mbox{ si $v(\phi_1)=0$ , } \\ 1 &\mbox{ si $v(\phi_1)>0$ . } \end{array}\right.$

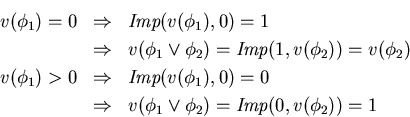
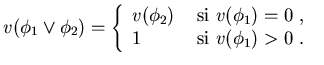
En consecuencia, la disyunción puede no ser conmutativa.

Es menester pues introducir de alguna otra forma a los conectivos.

Dado un operador conjuntor que ``no tenga saltos'' es posible reconstruir a los operadores Máximo y Mínimo. La demostración es puramente técnica (consiste de hecho en la comprobación de algunas desigualdades) y por eso la omitimos:

Observación 3.2   Sea $\diamond:[0,1]^2\rightarrow[0,1]$ un operador conjuntor contínuo. Entonces:

1.

$\forall x,y\in[0,1]:\ \ \mathop{\rm Min}\{x,y\}=x\diamond\mbox{\it Imp}(x,y)$.

2.

$\forall x,y\in[0,1]:\ \ \mathop{\rm Max}\{x,y\}=\mathop{\rm Min}\{ \mbox{\it Imp}(\mbox{\it Imp}(x,y),y) , \mbox{\it Imp}(\mbox{\it Imp}(y,x),x) \}$.

Asociemos el operador conjuntor a un conectivo ``conjunción fuerte'' y definamos a los demás, incluído uno ``disyunción fuerte'', como sigue:

$$\begin{eqnarray*}v(\neg \phi) &=& \mbox{\it Imp}(v(\phi),0) \\ v(\phi_1\& \phi... ...(\phi_1),v(\phi_2))\diamond \mbox{\it Imp}(v(\phi_2),v(\phi_1)) \end{eqnarray*}$$

En tal caso, tendremos las equivalencias lógicas:

$$\begin{eqnarray*}\phi_1\land \phi_2 &\equiv& \phi_1\&(\phi_1\rightarrow \phi_2) ... ...&\equiv& (\phi_1\rightarrow \phi_2)\& (\phi_2\rightarrow \phi_1) \end{eqnarray*}$$

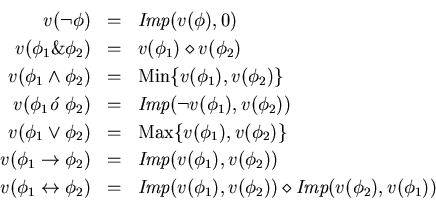
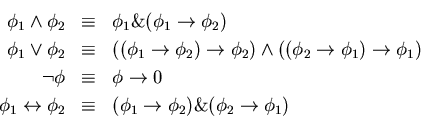
Así pues, utilizando un operador conjuntor (contínuo) es posible construir un cálculo proposicional difuso. Veamos algunos ejemplos de este tipo de construcción:

Gödel.

Consideremos el operador conjuntor $x\diamond y=\mathop{\rm Min}\{x,y\}$. Para cualesquiera dos números $x,y\in [0,1]$se tiene, $\forall z\in [0,1]$:

$$z\diamond x\leq y \ \Leftrightarrow \ \left\{\begin{array}{lc... ...leq z &\Rightarrow& x\leq y \hspace{2cm} (2) \end{array}\right.$$

Observamos que si $x\leq y$, la implicación (1) se cumple para cualquier z, y la implicación (2) se cumple porque su consecuente es verdadero. En tanto que si x>y, la implicación (1) se cumple para cualquier $z\leq y$, y también para tales z se cumplirá la implicación (2), pues tanto su antecedente como su consecuente serán falsos.

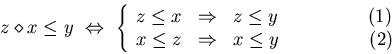
Consecuentemente, $\mbox{\it Imp}(x,y)=\left\{\begin{array}{ll} 1 &\mbox{ si $x\leq y$ , } \\ y &\mbox{ si $x>y$ . } \end{array}\right.$

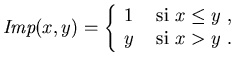
Los valores de verdad de los conectivos quedan entonces definidos como en el recuadro (11),

  

Table 11: Conectivos resultantes del conjuntor de Gödel.

y sus gráficas pueden ser vistas en la figura 18.

  

Figure 18: Operadores composicionales de Gödel.

Producto-F.

Consideremos el operador conjuntor $x\diamond y=xy$. Para cualesquiera dos números $x,y\in [0,1]$ se tiene, $\forall z\in [0,1]$:

$$z\diamond x\leq y \ \Leftrightarrow \ (x=0) \lor\left(x\not=0\Rightarrow z\leq \frac{y}{x}\right)$$

Consecuentemente, $\mbox{\it Imp}(x,y)=\left\{\begin{array}{ll} 1 &\mbox{ si $x=0$ o $x\leq y$ , } \\ \frac{y}{x} &\mbox{ en otro caso. } \end{array}\right.$

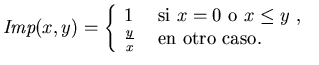
Los valores de verdad de los conectivos quedan entonces definidos como en el recuadro (12),

  

Table 12: Conectivos resultantes del conjuntor producto.

y sus gráficas pueden ser vistas en la figura 19.

  

Figure 19: Operadores composicionales de Producto-F.

ukasiewicz.

Consideremos el operador conjuntor $x\diamond y=\mathop{\rm Max}\{x+y-1,0\}$. Observemos que este operador no satisface la relación (9), es decir, en este operador sí hay divisores de cero.

Para cualesquiera dos números $x,y\in [0,1]$ se tiene, $\forall z\in [0,1]$:

$$z\diamond x\leq y \ \Leftrightarrow \ 1-x\leq z\leq y+1-x$$

Consecuentemente, $\mbox{\it Imp}(x,y)=\mathop{\rm Min}\{1+y-x,1\}$.

Los valores de verdad de los conectivos quedan entonces definidos como en el recuadro (13),

  

Table: Conectivos resultantes del conjuntor de ukasiewicz.

y sus gráficas pueden ser vistas en la figura 20.

  

Figure: Operadores composicionales de ukasiewicz-F.

Siguiente: Semánticas basadas en implicación Un nivel arriba: Lógicas proposicionales difusas Anterior: Semánticas basadas en conjunción