Sea ![]() un espacio vectorial sobre el campo
un espacio vectorial sobre el campo ![]() de los números complejos. Denotemos por
de los números complejos. Denotemos por ![]() al espacio de transformaciones lineales de
al espacio de transformaciones lineales de ![]() en
en ![]() . El dual del espacio
. El dual del espacio ![]() es
es
![]() . Si
. Si ![]() escribimos, para cada
escribimos, para cada ![]() ,
,
![]() .
.
![]() es una transformación bilineal.
es una transformación bilineal.
Sea ![]() otro espacio vectorial también sobre
otro espacio vectorial también sobre ![]() . El producto tensorial de
. El producto tensorial de ![]() con
con ![]() es
es
![]() . Se tiene:
. Se tiene:
En efecto, consideremos
![]() tal que
tal que
![]() ,
,
![]() es la transformación
es la transformación
![]() . Claramente
. Claramente ![]() es bilineal. Se tiene que
es bilineal. Se tiene que
![]() si y sólo si existe
si y sólo si existe
![]() tal que
tal que
![]() . Esta última condición define una relación de equivalencia
. Esta última condición define una relación de equivalencia ![]() en
en ![]() . Así pues, el espacio cociente
. Así pues, el espacio cociente
![]() se identifica con un subespacio de
se identifica con un subespacio de ![]() . De hecho, la aplicación
. De hecho, la aplicación
![]() se denota como
se denota como
![]() y se dice ser el producto tensorial del vector
y se dice ser el producto tensorial del vector ![]() con el vector
con el vector ![]() . Debido a la linealidad de los operadores involucrados se tiene que valen las relaciones siguientes:
. Debido a la linealidad de los operadores involucrados se tiene que valen las relaciones siguientes:
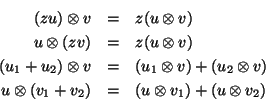
En efecto, si ![]() es de dimensión finita, entonces su dual
es de dimensión finita, entonces su dual ![]() es de la misma dimensión,
es de la misma dimensión, ![]() , y obviamente
, y obviamente
![]() .
.
Así pues, si
![]() y
y
![]() entonces, prácticamente,
entonces, prácticamente,
![]() .
.
En efecto,
![]() es una base del dual
es una base del dual ![]() , donde
, donde
![]() . Ahora, respecto a las bases
. Ahora, respecto a las bases ![]() y
y ![]() , la aplicación
, la aplicación
![]() se representa mediante la matriz
se representa mediante la matriz
![]() , donde
, donde
![]() si y sólo si
si y sólo si
![]() y
y
![]() si y sólo si
si y sólo si
![]() .
De manera un poco más general, escribamos cada
.
De manera un poco más general, escribamos cada ![]() como
como
![]() y
y
![]() , también cada
, también cada ![]() como
como
![]() . En consecuencia,
. En consecuencia,
![]() , y
, y
![]() .
.