



Siguiente: Lenguajes libres de contexto
Un nivel arriba: Formas normales
Anterior: Forma normal de Chomsky
Una gramática libre de contexto
G=(V,T,P,S) se dice estar en forma normal de Greibach si sus producciones son de la forma
Veremos que la construcción de formas normales de Greibach equivalentes a gramáticas dadas es procedimental.
Para cualquier gramática libre de contexto G, definamos, para cada variable  ,
a los conjuntos siguientes:
,
a los conjuntos siguientes:
Primeramente observemos que podemos ``componer producciones'' de manera que tengamos siempre una gramática equivalente a la gramática dada.
Lema 3.1 (Composición de producciones)
Si
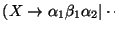
es una producción en
G y las producciones en
P(
Y) pueden escribirse como

entonces al sustituir
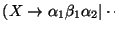
por las producciones
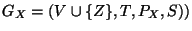
,
obtenemos una gramática equivalente a
G.
En efecto, en toda derivación terminal que aplique en un momento la producción
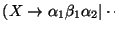 ,
necesariamente se ha de aplicar una producción en P(Y) para suprimir el símbolo Y.
,
necesariamente se ha de aplicar una producción en P(Y) para suprimir el símbolo Y.
Lema 3.2 (Transformación de producciones ``reflexivas'')
Para cada variable
enumeremos
Q(
X) y
R(
X) como
Sea
Z una variable que no ocurra en
V. Sea
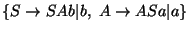
la gramática que se obtiene al sustituir el conjunto de producciones
P(
X) por las producciones
En efecto, toda derivación siniestra, en la gramática original, de una palabra en L(G) ha de determinar una derivación diestra de la misma palabra en la gramática transformada.
La demostración de la afirmación anterior es directa. Como mera ilustración, consideremos tan solo un ejemplo:
La gramática con producciones
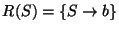 genera al lenguaje consistente de las palabras de la forma b(ab)*. De acuerdo con la construcción anterior, como
genera al lenguaje consistente de las palabras de la forma b(ab)*. De acuerdo con la construcción anterior, como
 y
y
 ,
obtenemos la gramática
,
obtenemos la gramática
Presentemos sendas derivaciones, siniestra en la gramática original y diestra en la transformada, para la palabra bababab:
Veamos ahora el resultado principal de esta sección:
Proposición 3.2
Toda gramática libre de contexto
G=(V,T,P,S) que no genere a la palabra vacía se puede transformar en una gramática libre de contexto
G*=(V*,T,P*,S*) en forma normal de Greibach.
Sea pues
G=(V,T,P,S) una gramática libre de contexto que no genere a
 .
La transformación a una forma normal de Greibach la hacemos gradualmente mediante los pasos siguientes:
.
La transformación a una forma normal de Greibach la hacemos gradualmente mediante los pasos siguientes:
- 1.
- Sea
G'=(V',T,P',S') la forma normal de Chomsky de G.
- 2.
- Modificaremos a las producciones en P' para tenerlas tales que toda producción, cuyo consecuente se inicie con una variable, ha de ser de la forma
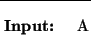 con j>i, para un cierto orden en el conjunto de variables actuales, digamos
con j>i, para un cierto orden en el conjunto de variables actuales, digamos
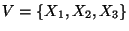 .
Para esto apliquemos el procedimiento cuyo seudocódigo se presenta en la figura 6.3.
.
Para esto apliquemos el procedimiento cuyo seudocódigo se presenta en la figura 6.3.
Figure 6.3:
Modificaciónde producciones de acuerdo con el orden de V'.
|
|
Por lo visto en el lema 6.3.2, la gramática G'' así obtenida es equivalente a G.
- 3.
- Ahora, hecha la transformación anterior, se tiene que
- la última variable Xm sólo puede ser antecedente de producciones cuyos consecuentes se inician con símbolos terminales,
- las producciones en
P(Xm-1) cuyos consecuentes se inician con Xm pueden transformarse, siguiendo el lema 6.3.1 de ``Composición de producciones'', en producciones equivalentes cuyos consecuentes se inician con símbolos terminales,
- de manera sucesiva para i=m-2 hasta i=1 las producciones en P(Xi) cuyos consecuentes se inician con algún Xj, con j>i, pueden transformarse, siguiendo el lema 6.3.1 de ``Composición de producciones'', en producciones equivalentes cuyos consecuentes se inician con símbolos terminales.
Con todas estas transformaciones la gramática resultante
G*=(V*,T,P*,S*) es, en efecto, equivalente a G y está en forma normal de Greibach.
Ejemplo:
Consideremos la gramática con símbolos variables
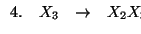 y producciones
y producciones
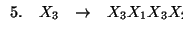
la cual ya está en forma normal de Chomsky.
Transformémosla de acuerdo con el procedimiento anterior.
Observemos que las dos primeras producciones ya tienen el tipo de las buscadas en el paso 2. del procedimiento anterior. La tercera tiene un consecuente que se inicia con un símbolo variable anterior al de su propio antecedente. Compongamos pues la producción 3. con la 1. Obtenemos
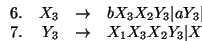
la cual también tiene un consecuente que se inicia con un símbolo variable anterior al de su propio antecedente. Compongamos pues la producción 4. con la 2. Obtenemos
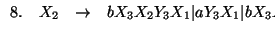
la cual es del tipo ``reflexivo''. Para transformarla, introduzcamos una nueva variable Y3. Obtenemos
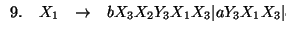 Con esto terminamos el paso 2. del procedimiento anterior. El conjunto actual de producciones consta de las producciones 1., 2., 6. y 7. Pasemos pues al paso 3. del procedimiento.
Sustituyendo 6. en 2. obtenemos
Con esto terminamos el paso 2. del procedimiento anterior. El conjunto actual de producciones consta de las producciones 1., 2., 6. y 7. Pasemos pues al paso 3. del procedimiento.
Sustituyendo 6. en 2. obtenemos
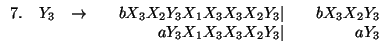 Sustituyendo 8. en 1. obtenemos
Sustituyendo 8. en 1. obtenemos
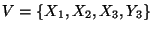 Sustituyendo 9. en 7. obtenemos 10 nuevas producciones
Sustituyendo 9. en 7. obtenemos 10 nuevas producciones
![$\begin{array}{lrcl}
7. & Y_3 &\rightarrow& \begin{array}[t]{rr}\begin{array}[t...
...ert \\ aX_1X_3X_3X_2\vert \\ bX_3X_3X_2 \
\end{array}\end{array}
\end{array}$](img1957.gif) En resumen, la gramática equivalente, en forma normal de Greibach, tiene como conjunto de variables a
En resumen, la gramática equivalente, en forma normal de Greibach, tiene como conjunto de variables a
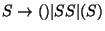 y sus producciones son la 6., 8., 9. y 10.:
y sus producciones son la 6., 8., 9. y 10.:
Ejemplo ``Cadenas equilibradas de paréntesis'':
Consideremos la gramática
 que genera a las cadenas equilibradas de paréntesis (CEP).
La forma normal de Chomsky de la gramática dada es
que genera a las cadenas equilibradas de paréntesis (CEP).
La forma normal de Chomsky de la gramática dada es
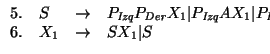 Consideremos el siguiente orden de las variables:
Consideremos el siguiente orden de las variables:
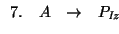 .
La producción 1. es ``reflexiva''. Introduzcamos una nueva variable, X1. Al hacer la transformación pertinente, obtenemos:
.
La producción 1. es ``reflexiva''. Introduzcamos una nueva variable, X1. Al hacer la transformación pertinente, obtenemos:
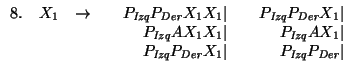 La producción 4. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 4. con 5. obtenemos
La producción 4. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 4. con 5. obtenemos
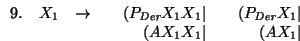 La producción 6. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 6. con 5. obtenemos
La producción 6. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 6. con 5. obtenemos
![$\begin{array}{llcl}
8. & X_1 &\rightarrow& \begin{array}[t]{rr}\begin{array}[t...
...\vert \\ P_{\mbox{\scriptsize\it Izq}}A \
\end{array}\end{array}
\end{array}$](img1965.gif) Al componer 8. con 2. obtenemos
Al componer 8. con 2. obtenemos
![$\begin{array}{llcl}
9. & X_1 &\rightarrow& \begin{array}[t]{rr}\begin{array}[t...
..._{\mbox{\scriptsize\it Der}}\vert \\ (A \
\end{array}\end{array}
\end{array}$](img1966.gif) En este momento, en nuestro conjunto actual de producciones 2., 3., 5., 7. y 9., ningún consecuente se inicia con alguna variable que anteceda a la variable en el antecedente de la producción correspondiente.
En el paso 3. del procedimiento para obtener formas normales de Greibach, hemos de sustituir la variable
En este momento, en nuestro conjunto actual de producciones 2., 3., 5., 7. y 9., ningún consecuente se inicia con alguna variable que anteceda a la variable en el antecedente de la producción correspondiente.
En el paso 3. del procedimiento para obtener formas normales de Greibach, hemos de sustituir la variable
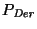 por el símbolo (, según la producción 2., toda vez que aparezca al inicio del consecuente de alguna producción. Obtenemos así la gramática:
por el símbolo (, según la producción 2., toda vez que aparezca al inicio del consecuente de alguna producción. Obtenemos así la gramática:
Y esta gramática ya queda en forma normal de Greibach. Observemos que la variable
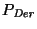 es irrelevante. De hecho si hacemos la sustitución del otro símbolo
es irrelevante. De hecho si hacemos la sustitución del otro símbolo
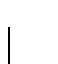 obtenemos la gramática equivalente
obtenemos la gramática equivalente
que también está en forma normal de Greibach.




Siguiente: Lenguajes libres de contexto
Un nivel arriba: Formas normales
Anterior: Forma normal de Chomsky
Guillermo Morales-Luna
2000-06-27
 ,
a los conjuntos siguientes:
,
a los conjuntos siguientes:
 entonces al sustituir
entonces al sustituir
 enumeremos Q(X) y R(X) como
enumeremos Q(X) y R(X) como
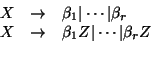
 y
y
 ,
obtenemos la gramática
,
obtenemos la gramática
![$\begin{array}{lrcl}
7. & Y_3 &\rightarrow& \begin{array}[t]{rr}\begin{array}[t...
...ert \\ aX_1X_3X_3X_2\vert \\ bX_3X_3X_2 \
\end{array}\end{array}
\end{array}$](img1957.gif) En resumen, la gramática equivalente, en forma normal de Greibach, tiene como conjunto de variables a
En resumen, la gramática equivalente, en forma normal de Greibach, tiene como conjunto de variables a
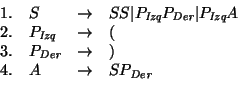
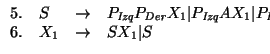 Consideremos el siguiente orden de las variables:
Consideremos el siguiente orden de las variables:
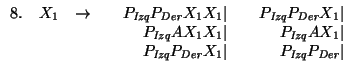 La producción 4. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 4. con 5. obtenemos
La producción 4. tiene un consecuente que se inicia con una variable anterior a su antecedente. Al componer 4. con 5. obtenemos
![$\begin{array}{llcl}
9. & X_1 &\rightarrow& \begin{array}[t]{rr}\begin{array}[t...
..._{\mbox{\scriptsize\it Der}}\vert \\ (A \
\end{array}\end{array}
\end{array}$](img1966.gif) En este momento, en nuestro conjunto actual de producciones 2., 3., 5., 7. y 9., ningún consecuente se inicia con alguna variable que anteceda a la variable en el antecedente de la producción correspondiente.
En el paso 3. del procedimiento para obtener formas normales de Greibach, hemos de sustituir la variable
En este momento, en nuestro conjunto actual de producciones 2., 3., 5., 7. y 9., ningún consecuente se inicia con alguna variable que anteceda a la variable en el antecedente de la producción correspondiente.
En el paso 3. del procedimiento para obtener formas normales de Greibach, hemos de sustituir la variable
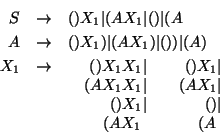
 obtenemos la gramática equivalente
obtenemos la gramática equivalente