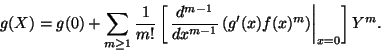![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) tiene una estructura de anillo conmutativo con la suma y el producto convencionales de series.
Más aún, forma un dominio entero:
tiene una estructura de anillo conmutativo con la suma y el producto convencionales de series.
Más aún, forma un dominio entero:
Además, los elementos invertibles en
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) son aquellos cuyo coeficiente ``independiente'' no es nulo:
son aquellos cuyo coeficiente ``independiente'' no es nulo:
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) a la colección de todas las series racionales sobre
a la colección de todas las series racionales sobre
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) tiene una estructura de anillo conmutativo con la suma y el producto convencionales de series.
Más aún, forma un dominio entero:
tiene una estructura de anillo conmutativo con la suma y el producto convencionales de series.
Más aún, forma un dominio entero:
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) son aquellos cuyo coeficiente ``independiente'' no es nulo:
son aquellos cuyo coeficiente ``independiente'' no es nulo:
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) es posible , bajo determinadas circunstancias, resolver ecuaciones de la forma
es posible , bajo determinadas circunstancias, resolver ecuaciones de la forma
En efecto,
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) .
.
 ,
donde cada coeficiente ak es una forma polinomial en Y, se resuelve mediante un sistema de ecuaciones recurrentes.
,
donde cada coeficiente ak es una forma polinomial en Y, se resuelve mediante un sistema de ecuaciones recurrentes.
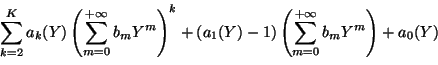
 ,
donde para cada
,
donde para cada 
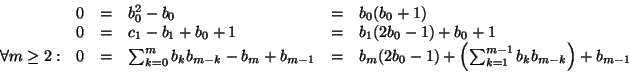
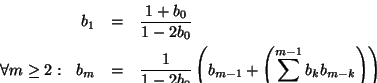
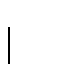 ,
,
 se tiene que la expresión g(X) satisface la ecuación
se tiene que la expresión g(X) satisface la ecuación
 .
Dada la función g, se busca expresar a g(X) como una serie de potencias en Y, es decir, se busca coeficientes
.
Dada la función g, se busca expresar a g(X) como una serie de potencias en Y, es decir, se busca coeficientes
 tales que
tales que
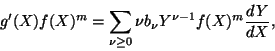

 se tiene
se tiene
 .
Ahora bien,
.
Ahora bien,
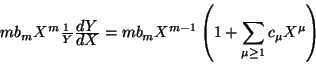
 se observa que el término
se observa que el término