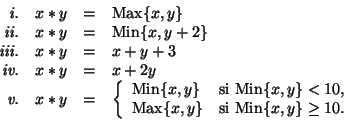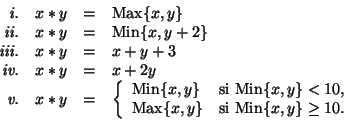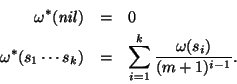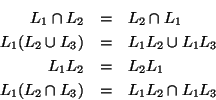Siguiente: Gramáticas formales
Un nivel arriba: Fundamentos matemáticos
Anterior: Propiedades de cerradura
1. Proporcione tres ejemplos de monoides finitos mostrando sus respectivas tablas de operación.
2. En cada una de las operaciones definidas a continuación, sobre el conjunto de número naturales
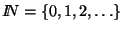 ,
decida si es acaso asociativa o si posee una unidad lateral:
,
decida si es acaso asociativa o si posee una unidad lateral:
3. Sea S un conjunto no vacío dotado de una operación binaria
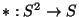 tal que
tal que
Muestre que * es una operación asociativa.
4. Suponga que en un monoide (S,*) se cumplen las relaciones siguientes:
Muestre que entonces se cumple la relación
Dé un ejemplo que ilustre este ejercicio.
5. Sea (S,*) un monoide y 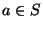 un elemento cualquiera. Se define una nueva operación ``
un elemento cualquiera. Se define una nueva operación `` '' haciendo
'' haciendo
Muestre que esta nueva operación es asociativa. Dé condiciones sobre a suficientes para que esta operación posea unidad, y en tal caso caracterice a las unidades.
6. Muestre que si (S,*) es una estructura asociativa finita, entonces posee un elemento idempotente, es decir,
7. Sea n>1 un entero positivo. Para cada entero x sea
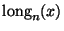 el mínimo entero k tal que nk>x.
el mínimo entero k tal que nk>x.
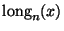 se dice ser la longitud de x en base n.
Dados
se dice ser la longitud de x en base n.
Dados
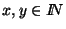 definimos
definimos
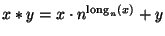 .
Pruebe que
.
Pruebe que
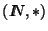 es un monoide.
es un monoide.
8. Sean R y S dos relaciones de equivalencia sobre un conjunto dado. Sea 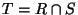 ,
es decir,
,
es decir,
a) Pruebe que T es una relación de equivalencia.
b) Exprese al índice de T en términos de los índices de R y S.
c) Sea 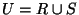 .
Decida si acaso U es una relación de equivalencia y justifique su decisión.
.
Decida si acaso U es una relación de equivalencia y justifique su decisión.
9. En 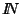 ,
considere la relación,
,
considere la relación,
Decida si acaso R es reflexiva, o simétrica, o transitiva, o antisimétrica, o de equivalencia o de orden.
10. En (0+1)*, considere la relación,
Decida si acaso R es reflexiva, o simétrica, o transitiva, o antisimétrica, o de equivalencia o de orden.
11. En un conjunto de 10 elementos,
a) cuente el número de relaciones simétricas y bosqueje un procedimiento para generar a todas ellas, una a una,
b) cuente el número de relaciones reflexivas y bosqueje un procedimiento para generar a todas ellas, una a una,
c) cuente el número de relaciones transitivas y bosqueje un procedimiento para generar a todas ellas, una a una.
12. Sea R una relación de equivalencia y sea
Pruebe que S es una relación de equivalencia. Compare el índice de S con el de R.
13. Dé un ejemplo de una relación definida sobre algún conjunto que sea simétrica y transitiva mas no reflexiva.
14. Dos palabras
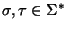 se dicen conjugadas si
se dicen conjugadas si
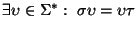 .
Pruebe que dos palabras
.
Pruebe que dos palabras
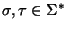 son conjugadas si y sólo si
son conjugadas si y sólo si
15. Muestre que la relación de conjugación es una relación de equivalencia en el diccionario de cualquier alfabeto.
16. Muestre que si
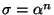 ,
donde
,
donde
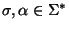 y
y 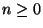 ,
entonces cualquier conjugado de
,
entonces cualquier conjugado de  es de la forma
es de la forma
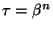 ,
donde
,
donde 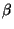 es un conjugado de
es un conjugado de 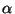 .
.
17. Sea 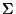 un alfabeto con m>0 símbolos. Sea
un alfabeto con m>0 símbolos. Sea
![$\omega:\Sigma \rightarrow [1,m]$](img380.gif) una enumeración de
una enumeración de 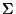 .
Se tiene un orden natural en
.
Se tiene un orden natural en 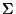 :
:
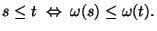 a) Extendemos
a) Extendemos 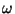 a una función
a una función
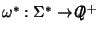 ,
donde
,
donde
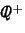 es el conjunto de números racionales positivos, haciendo
es el conjunto de números racionales positivos, haciendo
Decida si acaso 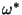 es una biyección.
b) Pruebe que la relación
es una biyección.
b) Pruebe que la relación
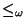 en
en 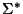 definida como
definida como
es una relación de orden en 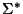 que coincide con el orden lexicográfico inducido por
que coincide con el orden lexicográfico inducido por 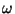 en
en 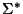 .
c) ¿Si se definiera
.
c) ¿Si se definiera
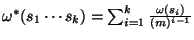 ,
podría concluirse lo mismo que en el inciso anterior ?
,
podría concluirse lo mismo que en el inciso anterior ?
18.
Decida cuáles de las siguientes relaciones se cumplen para cualesquiera tres lenguajes
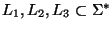 :
:
19. Sea
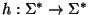 un homomorfismo. Decida cuáles de las siguientes relaciones se cumplen para cualesquiera dos lenguajes
un homomorfismo. Decida cuáles de las siguientes relaciones se cumplen para cualesquiera dos lenguajes
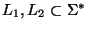 :
:
20. Sea
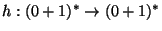 el homomorfismo tal que
h(0)=1,h(1)=01. Sea
el homomorfismo tal que
h(0)=1,h(1)=01. Sea
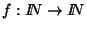 la función
la función
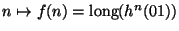 .
Dé una expresión aritmética para calcular f. Demuestre la validez de su expresión.
.
Dé una expresión aritmética para calcular f. Demuestre la validez de su expresión.




Siguiente: Gramáticas formales
Un nivel arriba: Fundamentos matemáticos
Anterior: Propiedades de cerradura
Guillermo Morales-Luna
2000-06-27