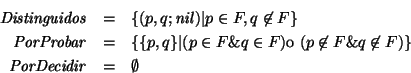Siguiente: Autómatas no-deterministas Un nivel arriba: Cocientes de autómatas Anterior: Congruencias de autómatas

Indistinguibilidad de estados en autómatas

Otro ejemplo, muy importante, de congruencias de autómatas está dado por la noción de indistinguibilidad. Para un autómata $\mbox{\it AF\/}=(Q,\mbox{\it Ent\/},\mbox{\it tran\/},q_0,F)$ definimos la siguiente relación en Q:

$$\forall p,q\in Q:\ \ p\equiv_{\mbox{\scriptsize\it Ind}} q\ \... ... F\ \ \Leftrightarrow\ \ \mbox{\it tran\/}^*(q,\sigma)\in F]$$ (10)

es decir, dos estados son indistinguibles cuando y sólo cuando ante mismas entradas o bien ambos transitan a estados finales o bien ninguno de los dos lo hace. Es evidente que `` $\equiv_{\mbox{\scriptsize\it Ind}}$'' es una relación de equivalencia. Además, como $\mbox{\it Ent\/}^*=\mbox{\it Ent\/}\cdot\mbox{\it Ent\/}^*$, se tiene,

$$p\equiv_{\mbox{\scriptsize\it Ind}} q\ \ \Leftrightarrow\ \ \... ...(p,e)\equiv_{\mbox{\scriptsize\it Ind}} \mbox{\it tran\/}(q,e).$$

Por tanto `` $\equiv_{\mbox{\scriptsize\it Ind}}$'' es también una congruencia, y en consecuencia se puede construir el autómata cociente $\left(\mbox{\it AF\/}/\equiv_{\mbox{\scriptsize\it Ind}}\right)$. Más aún,

$$q_1\in F\ \&\ \left(q_1\equiv_{\mbox{\scriptsize\it Ind}} q_2... ... nil\/})\in F\right)\ \&\ q_1\in F \ \ \Rightarrow \ \ q_2\in F$$

así que F es una unión de clases de indistinguibilidad. Consecuentemente se tiene la

Observación 2.4   El autómata $\mbox{\it AF\/}$ es equivalente a su cociente $\left(\mbox{\it AF\/}/\equiv_{\mbox{\scriptsize\it Ind}}\right)$.

Observemos que es posible trasladar la relación de equivalencia `` $\equiv_{\mbox{\scriptsize\it Ind}}$'' a una relación `` $\equiv_{\mbox{\scriptsize\it Ind, AF}}$'' en el diccionario $\mbox{\it Ent\/}^*$ haciendo

$$\forall \sigma_1,\sigma_2\in \mbox{\it Ent\/}^*:\ \ \sigma_1\... ...\ \ T(\sigma_1)\equiv_{\mbox{\scriptsize\it Ind}}T(\sigma_2)$$ (11)

la cual es invariante por la derecha.

Observación 2.5   La relación `` $\approx_{\mbox{\scriptsize\it AF}}$'' es un refinamiento de la relación `` $\equiv_{\mbox{\scriptsize\it Ind, AF}}$'', es decir,

$$\forall\sigma_1,\sigma_2\in \mbox{\it Ent\/}^*:\ \ \sigma_1\a... ...tarrow\ \sigma_1\equiv_{\mbox{\scriptsize\it Ind, AF}}\sigma_2.$$

En efecto, si $\sigma_1\approx_{\mbox{\scriptsize\it AF}}\sigma_2$ se tiene $T(\sigma_1)=T(\sigma_2)$ y al ser `` $\equiv_{\mbox{\scriptsize\it Ind, AF}}$'' reflexiva, $T(\sigma_1)\equiv_{\mbox{\scriptsize\it Ind}}T(\sigma_2)$. Por tanto, el cociente $\left(\mbox{\it Ent\/}^*/\equiv_{\mbox{\scriptsize\it Ind, AF}}\right)$, que prácticamente coincide con el cociente $\left(\mbox{\it AF\/}/\equiv_{\mbox{\scriptsize\it Ind}}\right)$, es de cardinalidad menor o igual que la cardinalidad del autómata AF. Veremos que el cociente $\left(\mbox{\it AF\/}/\equiv_{\mbox{\scriptsize\it Ind}}\right)$ puede ser visto como ``un buen representante'' de la clase de autómatas equivalentes al autómata $\mbox{\it AF\/}$. Sean $\mbox{\it AF\/}_1=(Q_1,\mbox{\it Ent\/},\mbox{\it tran\/}_1,q_{10}, F_1)$ y $\mbox{\it AF\/}_2=(Q_2,\mbox{\it Ent\/},\mbox{\it tran\/}_2,q_{20}, F_2)$ dos autómatas equivalentes.

Lema 2.3   Las relaciones `` $\equiv_{\mbox{\scriptsize\it Ind, AF}_1}$'' y `` $\equiv_{\mbox{\scriptsize\it Ind, AF}_2}$'' coinciden.

En efecto, las siguientes equivalencias lógicas son evidentes:

$$\begin{eqnarray*}\sigma_1\equiv_{\mbox{\scriptsize\it Ind, AF}_1}\sigma_2 &\Left... ...arrow& \sigma_1\equiv_{\mbox{\scriptsize\it Ind, AF}_2}\sigma_2 \end{eqnarray*}$$

Resulta entonces el

Corolario 2.1   Los autómatas cocientes $\left(\mbox{\it AF\/}_1/\equiv_{\mbox{\scriptsize\it Ind}}\right)$ y $\left(\mbox{\it AF\/}_2/\equiv_{\mbox{\scriptsize\it Ind}}\right)$ son isomorfos.

En efecto, ambos son isomorfos al cociente $\left(\mbox{\it Ent\/}^*/\equiv_{\mbox{\scriptsize\it Ind, AF}_i}\right)$, sin importar cuál de los dos i=1,2. De todo esto resulta la siguiente proposición que explica porqué es que el autómata cociente es un buen representante de los autómatas equivalentes.

Proposición 2.3 (Propiedad universal)   Si $\mbox{\it AF\/}_1$ es equivalente a $\mbox{\it AF\/}_2$ entonces $\left(\mbox{\it AF\/}_1/\equiv_{\mbox{\scriptsize\it Ind}}\right)$ es una imagen homomorfa de $\mbox{\it AF\/}_2$.

Corolario 2.2 (Minimización)   El cociente $\left(\mbox{\it AF\/}_1/\equiv_{\mbox{\scriptsize\it Ind}}\right)$ es el autómata mínimo, en cuanto al número de estados, entre todos los equivalentes al autómata $\mbox{\it AF\/}_1$.

Para finalizar esta sección presentaremos un procedimiento para calcular el autómata cociente $\left(\mbox{\it AF\/}/\equiv_{\mbox{\scriptsize\it Ind}}\right)$, dado el autómata $\mbox{\it AF\/}$. Sea pues $\mbox{\it AF\/}=(Q,\mbox{\it Ent\/},\mbox{\it tran\/},q_0,F)$ un autómata finito. Dos estados son distinguibles si ellos no son indistinguibles. Observamos lo siguiente:

1.

Si un estado es final y otro no lo es, esos dos estados son distinguibles, y la palabra vacía los distingue.

2.

Si dos estados p₁, p₂ son distinguibles y la palabra $\tau$ los distingue, y si para un símbolo $e\in\mbox{\it Ent\/}$ y algunos otros estados q₁, q₂ se tiene $\mbox{\it tran\/}(q_1,e) = p_1$ y $\mbox{\it tran\/}(q_2,e) = p_2$, entonces q₁ y q₂ son distinguibles y la palabra $e\tau$ los distingue.

Con estas observaciones podemos bosquejar un algoritmo para clasificar a las parejas de estados en aquellas que son distinguibles, con respectivas palabras distinguientes, y en aquellas que son indistinguibles. A grandes rasgos, a lo largo del proceso utilizaremos las listas siguientes:

Distinguidos	:	parejas de estados ya reconocidas como distinguibles. A cada una le asociamos la palabra que las distingue,
PorProbar	:	parejas de estados por ser aún probadas,
PorDecidir	:	parejas de estados que, aunque ya han sido probadas, la decisión de si acaso son distinguibles quedó relegada a una palabra aún por revisarse,

y procedemos como sigue:

1.

Inicialmente, las primeras parejas distinguidas son las formadas por un estado final y otro no-final y la palabra vacía es la que los distingue. Las demás parejas quedan por ser probadas y no hay parejas con decisión pendiente. Sean pues,

$$\begin{eqnarray*}\mbox{\it Distinguidos\/} &=& \{(p,q;\mbox{\it nil\/})\vert p\i... ...in F\&q\not\in F)\} \\ \mbox{\it PorDecidir\/} &=& \emptyset \end{eqnarray*}$$

2.

En tanto que haya parejas PorProbar: se toma una de estas parejas, digamos $\{p,q\}$. Se tiene dos posibilidades:

(a)

para cada símbolo e la pareja $\{p_e,q_e\}=\{\mbox{\it tran\/}(p,e),\mbox{\it tran\/}(p,e)\}$ no aparece en $\mbox{\it Distinguidos\/}$. Entonces $\{p,q\}$ se incorpora a $\mbox{\it PorDecidir\/}$ y para cada e, $\{p,q\}$ relega su decisión a la pareja $\{p_e,q_e\}$, o bien,

(b)

existe un símbolo e tal que para $\{p_e,q_e\}=\{\mbox{\it tran\/}(p,e),\mbox{\it tran\/}(p,e)\}$, hay una terceta $\{p_e,q_e;\sigma\}\in\mbox{\it Distinguidos\/}$. En tal caso, incorporamos $\{p,q;e\sigma\}$ a $\mbox{\it Distinguidos\/}$, y recursivamente todas las parejas que hayan relegado su decisión a $\{p,q\}$ se reconocen como distinguibles, y con las palabras que las distinguen se incorporan a $\mbox{\it Distinguidos\/}$,

3.

al final, las parejas indistinguibles son las que quedan en la lista $\mbox{\it PorDecidir\/}$.

Ejemplo. Consideremos el autómata $\mbox{\it AF21\/}=(\mbox{\it SAF21\/},F)$ de 21 estados cuyo semiautómata adyacente posee la función de transición que aparece en la tabla (3.8).

  

Table 3.8: Semiautómata SAF21.

y cuyo conjunto de estados finales es

$$F= \{q_{0}, q_{3}, q_{12}, q_{13}, q_{18}, q_{19}\}.$$

Al proceder de acuerdo con el algoritmo bosquejado para el cálculo de parejas de estados indistinguibles se reconoce a las parejas de estados distinguibles, con respectivas palabras distinguientes, mostradas en las tablas (3.9, 3.10).

  

Table 3.9: Primer grupo de parejas de estados distinguibles en el autómata AF21.

En cada renglón i<21 de la tabla (3.9) aparecen parejas de la forma $(q_{i'},q_i;\mbox{\it nil\/})$, donde i'<i y $(q_{i'},q_i)\in [F\times (Q-F)]\cup [(Q-F)\times F]$. Por tanto, es la palabra vacía la que distinge a esas parejas de estados.

  

Table 3.10: Segundo grupo de parejas de estados distinguibles en el autómata AF21.

Ahora bien, en cada renglón i<21 de la tabla (3.10) aparecen por lo general parejas de la forma $(q_{i'},q_i;\sigma)$, donde i'<i y $\sigma$ distinge a esa pareja de estados. Cuando llega a aparecer en ese renglón una pareja de la forma $(q_{j'},q_j;\sigma')$ con j<i, es porque en su momento, la pareja (q_j',q_j) relegó su decisión, respecto a indistinguibilidad, en una pareja de la forma (q_i',q_i). Por ejemplo en el renglón correspondiente a i=15 aparece la pareja (q₈,q₁₀) con la palabra 10, porque $\mbox{\it tran\/}(q_{8},1)=q_{15}$, $\mbox{\it tran\/}(q_{10},1)=q_{4}$ y recién se ha descubierto que la palabra 0 distingue a la pareja (q₄,q₁₅). También aquí aparece la pareja (q₄,q₁₄) con la palabra 110, porque $\mbox{\it tran\/}(q_{4},1)=q_{10}$, $\mbox{\it tran\/}(q_{14},1)=q_{8}$ y se acaba de descubrir que la palabra 10 distingue a la pareja (q₈,q₁₀). Las parejas de estados indistinguibles quedan enlistadas en la tabla (3.11).

  

Table 3.11: Parejas de estados indistinguibles en el autómata AF21.

Estas determinan una relación de equivalencia, cuyas clases aparecen, renombradas, en la tabla (3.12-a).

  

Table 3.12: Autómata cociente bajo la noción de indistinguibilidad en el autómata AF21.

Al considerar en ese espacio cociente la esctructura de semiautómata inducida por el semiautómata original se obtiene la función de transición de la tabla (3.12-b). Finalmente, ha de marcarse como estados finales a las clases p₀ y p₆, consistentes de estados finales en AF21, para obtener un autómata equivalente a AF21, que de acuerdo con el corolario 3.2.2 es el mínimo entre los equivalentes a AF21.
Siguiente: Autómatas no-deterministas Un nivel arriba: Cocientes de autómatas Anterior: Congruencias de autómatas