



Siguiente: Propiedades de cerradura
Un nivel arriba: Autómatas finitos y expresiones
Anterior: Autómatas bidireccionales
Sean
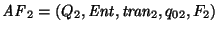 y
y
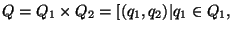 dos autómatas finitos. Su semiautómata producto se define sobre el producto cartesiano como sigue:
dos autómatas finitos. Su semiautómata producto se define sobre el producto cartesiano como sigue:
- estados:
-
![$Q=Q_1\times Q_2={[(q_1,q_2)\vert q_1\in Q_1,q_2\in Q_2]}$](img1169.gif) ,
,
- estado inicial:
-
q01=(q01,q02),
- transiciones:
-
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}:Q\times \mbox{\it Ent\/} &\rightarrow& ...
...=\left(\mbox{\it tran\/}_1(q_1,e),\mbox{\it tran\/}_2(q_2,e)\right)
\end{array}$](img1170.gif)
(se tiene un semiautómata porque aún no hay estados finales). Denotemos por
 a este semiautómata.
a este semiautómata.
Es evidente que
Así pues, si definimos como conjunto de estados finales al conjunto
entonces una palabra
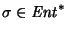 será reconocida por el producto si y sólo si lo es por alguno de los autómatas
será reconocida por el producto si y sólo si lo es por alguno de los autómatas
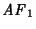 o
o
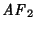 ,
es decir, en este caso,
,
es decir, en este caso,
Ahora, si definimos como conjunto de estados finales al conjunto
entonces una palabra
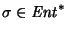 será reconocida por el producto si y sólo si lo es por ambos autómatas
será reconocida por el producto si y sólo si lo es por ambos autómatas
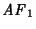 o
o
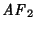 ,
es decir, en este caso,
,
es decir, en este caso,
Naturalmente, un autómata producto puede reducirse de manera equivalente considerando unicamente su parte accesible, es decir, aplicándole el algoritmo 3.5.
Guillermo Morales-Luna
2000-06-27
![]() y
y
![]() dos autómatas finitos. Su semiautómata producto se define sobre el producto cartesiano como sigue:
dos autómatas finitos. Su semiautómata producto se define sobre el producto cartesiano como sigue: