Hasta ahora los autómatas que hemos considerado leen su entrada de izquierda a derecha y no reculan sobre ella para realizar transiciones alternativas en función de la ``historia'' de la entrada. Los autómatas bidireccionales en cambio, sí pueden revisar la cadena de entrada y efectuar transiciones en función de una misma entrada leída varias veces. Veamos una formalización de esta noción de autómatas finitos.
Un autómata bidireccional es una estructura de la forma

La semántica del autómata es muy intuitiva: Si se está leyendo la i-ésima posición de una palabra de entrada, en la cual aparece el símbolo e, y se está en el estado q entonces,
Para llevar un recuento de las transiciones del autómata utilizaremos descripciones instantáneas (DI's). Una DI es una cadena
![$\sigma_{\mbox{\scriptsize\it Izq}}\begin{array}[t]{c} \underline{e} \\ \stackrel{\uparrow}{q} \end{array}\sigma_{\mbox{\scriptsize\it Der}},$](img1073.gif) o bien de la forma
o bien de la forma
Diremos que una DI
![]() se sigue de otra
se sigue de otra
![]() ,
,
![]() ,
si es el resultado de aplicar la transición correspondiente a d0. Formalmente,
,
si es el resultado de aplicar la transición correspondiente a d0. Formalmente,
![]()
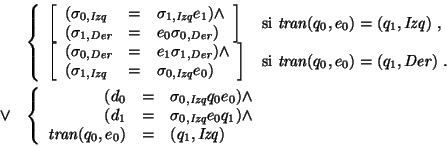
La cerradura reflexivo-transitiva de la relación ``se sigue'' es la relación ``se deriva'', denotada como
![]() .
.
Una palabra
![]() es reconocida por el autómata bidireccional
es reconocida por el autómata bidireccional
![]() si para algún estado final
si para algún estado final ![]() se tiene
se tiene
![]() .
Es decir, una palabra es reconocida si para cuando se concluya su lectura se haya arribado a un estado final. El lenguaje reconocido por el autómata bidireccional
.
Es decir, una palabra es reconocida si para cuando se concluya su lectura se haya arribado a un estado final. El lenguaje reconocido por el autómata bidireccional
![]() es
es
Un lenguaje es regular-B si es reconocido por un autómata bidireccional.
Ejemplo
El autómata bidireccional
![]() que
que
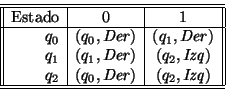
El estado inicial es q0.
Si q1 se designa como estado final, entonces se reconocerá a palabras de la forma
0*(010*)*010*.
Ejemplo
Consideremos el semiautómata bidireccional
![]() de 6 estados sobre el alfabeto de dos símbolos A=[a,b]:
de 6 estados sobre el alfabeto de dos símbolos A=[a,b]:

Una palabra que termina de leerse es
![]() .
En la tabla (3.16) se ve la acción de
.
En la tabla (3.16) se ve la acción de
![]() sobre
sobre ![]() .
.
Si se ve la entrada del autómata como inscrita en una cinta con casillas contiguas, en cada una de las cuales se inscribe un símbolo, entonces en una palabra de k símbolos habrá k+1 separadores de casillas.
Si la palabra de entrada fuese
![]() ,
al escribir explícitamente a los separadores, podríamos re-escribir a
,
al escribir explícitamente a los separadores, podríamos re-escribir a ![]() como
como
La aplicación de la palabra de entrada ![]() en el autómata determina una sucesión de cruce Si en cada uno de los separadores si, de acuerdo con la construcción siguiente:
en el autómata determina una sucesión de cruce Si en cada uno de los separadores si, de acuerdo con la construcción siguiente:
 y e está en la posición j, entonces
y e está en la posición j, entonces
Con estas reglas, toda sucesión de cruce ha de comenzar con una pareja de la forma
![]() correspondiente a un movimiento a la derecha, y los movimientos correspondientes a dos parejas sucesivas en una misma sucesión de cruce habrán de alternarse. Por tanto, al cabo de la lectura de una palabra de entrada, en cada separador, la correspondiente sucesión de cruce ha de tener un número impar de elementos. Además, en el caso de que se haya aplicado una palabra que es efectivamente reconocida, ninguna sucesión de cruce puede tener dos apariciones de una misma pareja (en otro caso la ``computación'' se ciclaría).
correspondiente a un movimiento a la derecha, y los movimientos correspondientes a dos parejas sucesivas en una misma sucesión de cruce habrán de alternarse. Por tanto, al cabo de la lectura de una palabra de entrada, en cada separador, la correspondiente sucesión de cruce ha de tener un número impar de elementos. Además, en el caso de que se haya aplicado una palabra que es efectivamente reconocida, ninguna sucesión de cruce puede tener dos apariciones de una misma pareja (en otro caso la ``computación'' se ciclaría).
Ejemplo
Para la palabra de longitud 6, 101001, las 7 sucesiones de cruce en el semiautómata bidireccional
![]() son las mostradas en la tabla 3.19.
son las mostradas en la tabla 3.19.
Ejemplo
Para la palabra de longitud 12,
![]() ,
las 13 sucesiones de cruce en el semiautómata bidireccional
,
las 13 sucesiones de cruce en el semiautómata bidireccional
![]() son las mostradas en la tabla 3.20.
son las mostradas en la tabla 3.20.
De manera general, diremos que una sucesión de cruce es una lista de parejas de la forma
![]() tal que
tal que
Por razones que se aclararán más adelante, diremos que una sucesión de cruce es derecha si comienza con un movimiento a la derecha y es de longitud impar. Simétricamente, diremos que es izquierda si comienza con un movimiento a la izquierda y es de longitud par.
Si hay n estados en el autómata bidireccional, entonces ninguna sucesión de cruce puede tener más de 2n elementos. Además, para cada ![]() hay
hay
![]() sucesiones de cruce de longitud 2j-1 que comiencen con el movimiento
sucesiones de cruce de longitud 2j-1 que comiencen con el movimiento
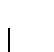 .
Por tanto, con n estados, hay
.
Por tanto, con n estados, hay

En resumen, el conjunto de sucesiones de cruce para un autómata bidireccional siempre es finito. Por esto, tendremos que todo autómata bidireccional será equivalente a uno finito no-determinista. Los estados de éste último serán precisamente las sucesiones de cruce derechas posibles. En lo que resta de esta sección, veremos cómo convertir un autómata bidireccional a uno finito equivalente.
Observemos en las tablas (3.19) y (3.20) que cualesquiera dos sucesiones de cruces contiguas ``concuerdan'' entre sí en el sentido de que sus construcciones son consistentes con el funcionamiento del correspondiente autómata bidireccional.
Ahora bien, diremos que dos sucesiones de cruce S1, S2 concuerdan para un símbolo
![]() si para alguna palabra
si para alguna palabra
![]() ,
en la cual e aparezca en una posición, digamos i, se tiene que S1 aparece como subcadena de la sucesión de cruce Si-1, S2 aparece como subcadena de Si y ambas cadenas forman la ``traza'' del funcionamiento del autómata bidireccional sobre la palabra
,
en la cual e aparezca en una posición, digamos i, se tiene que S1 aparece como subcadena de la sucesión de cruce Si-1, S2 aparece como subcadena de Si y ambas cadenas forman la ``traza'' del funcionamiento del autómata bidireccional sobre la palabra ![]() .
Diremos que S1 concuerda yendo a la derecha con S2 si la traza inicia con el primer elemento de S1 y el movimiento correspondiente es a la derecha. Similarmente, diremos que S2 concuerda yendo a la izquierda con S1 si la traza inicia con el primer elemento de S2 y el movimiento correspondiente es a la izquierda.
.
Diremos que S1 concuerda yendo a la derecha con S2 si la traza inicia con el primer elemento de S1 y el movimiento correspondiente es a la derecha. Similarmente, diremos que S2 concuerda yendo a la izquierda con S1 si la traza inicia con el primer elemento de S2 y el movimiento correspondiente es a la izquierda.
Para poner esto en términos más precisos:
En efecto, la pareja
![]() indica que se atraviesa al separador si-1 hacia la derecha para leer el símbolo e, y luego, por la acción del AB, se vuelve a atravesar si-1 pero ahora hacia la izquierda.
indica que se atraviesa al separador si-1 hacia la derecha para leer el símbolo e, y luego, por la acción del AB, se vuelve a atravesar si-1 pero ahora hacia la izquierda.
En efecto, estamos en una situación simétrica de la anterior.
En efecto, la pareja
![]() indica que se atraviesa a si-1 hacia la derecha para leer el símbolo e, y luego, por la acción del AB, se atraviesa si hacia la derecha también. Posteriormente para mantener la concordancia es necesario que S2 concuerde yendo a la izquierda con S1.
indica que se atraviesa a si-1 hacia la derecha para leer el símbolo e, y luego, por la acción del AB, se atraviesa si hacia la derecha también. Posteriormente para mantener la concordancia es necesario que S2 concuerde yendo a la izquierda con S1.
En efecto, estamos en una situación simétrica de la anterior.
En efecto, sea
![]() un autómata bidireccional. Construyamos el autómata no-determinista siguiente:
un autómata bidireccional. Construyamos el autómata no-determinista siguiente:
- estados:
,
- estado inicial:
,
- estados finales:
,
- transiciones:
Es fácil ver que ambos autómatas son equivalentes pues una ``computación reconocedora'', en el autómata no-determinista, corresponde a una lectura por columnas como las presentadas en las tablas 3.19 y 3.20, correspondientes a sendas ``computaciones reconocedoras'', en sus respectivos autómatas bidireccionales. El recíproco también vale.
El autómata descrito en la demostración anterior es muy extenso y seguramente ha de contener una gran cantidad de estados inaccesibles. Como una primera aproximación para reducir el tamaño del autómata equivalente podemos calcular sólo aquellas sucesiones de cruce que potencialmente pueden concordar, según lo permita la función de transición del autómata bidireccional.
Describamos un procedimiento que dado un símbolo a produce sendas listas de parejas de sucesiones de cruce que concuerdan yendo por la derecha, abreviado ConcDer, y yendo por la izquierda, abreviado ConcIzq, respecto al símbolo a. Para cada una de las dos relaciones, ConcDer y ConcIzq, utilizaremos un arreglo de palabras a revisar y otro de palabras ya revisadas.
El procedimiento descrito produce aún una gran cantidad de sucesiones de cruce, aunque efectivamente está descartando a muchísimas sucesiones irrelevantes.
Ejemplo
Volvamos al autómata
![]() .
El algoritmo anterior produce 48 parejas
de sucesiones de cruce derechas, de manera que la primera concuerda con la
segunda yendo a la derecha, respecto al símbolo 0. En la
tabla (3.22(a)) las enlistamos en su orden de aparición con el
algoritmo descrito. Sin embargo, ahí aparecen también sucesiones que
tienen elementos repetidos. En la tabla (3.22(b)) suprimimos esas
sucesiones.
.
El algoritmo anterior produce 48 parejas
de sucesiones de cruce derechas, de manera que la primera concuerda con la
segunda yendo a la derecha, respecto al símbolo 0. En la
tabla (3.22(a)) las enlistamos en su orden de aparición con el
algoritmo descrito. Sin embargo, ahí aparecen también sucesiones que
tienen elementos repetidos. En la tabla (3.22(b)) suprimimos esas
sucesiones.
![\begin{table}{\small
\begin{displaymath}\begin{array}{cc}
\begin{array}[b]{\vert...
...
\hline
\end{array} \\
(a) & (b)
\end{array}
\end{displaymath}}\end{table}](img1143.gif) |
En la tabla (3.23) enlistamos las parejas
de sucesiones de cruce derechas, de manera que la primera concuerda con la
segunda yendo a la derecha, respecto al símbolo 1, también en el orden de aparición con el algoritmo descrito.
Para el autómata
![]() ,
de 6 estados, este algoritmo da un número extremadamente grande de sucesiones relacionadas.
,
de 6 estados, este algoritmo da un número extremadamente grande de sucesiones relacionadas.
Como otra alternativa, en vez de generar todas las sucesiones de cruce plausibles, con cierta noción de plausibilidad, partiendo de la sucesión de cruce primera
![]() ,
dada una sucesión de cruce actual calcularemos a todas aquellas que concuerdan con ella yendo a la derecha para cada uno de los símbolos en el alfabeto de entrada.
,
dada una sucesión de cruce actual calcularemos a todas aquellas que concuerdan con ella yendo a la derecha para cada uno de los símbolos en el alfabeto de entrada.
Para esto, definimos dos relaciones
![]() y
y
 de manera tal que para cualesquiera dos sucesiones de cruce S y T:
de manera tal que para cualesquiera dos sucesiones de cruce S y T:
Diremos que una pareja
![]() es ``de zig-zag'', respecto al símbolo a si en la transición del autómata bidireccional se tiene
es ``de zig-zag'', respecto al símbolo a si en la transición del autómata bidireccional se tiene
![]() .
Diremos también que un estado q es un ``antecedente'' de
.
Diremos también que un estado q es un ``antecedente'' de
![]() si para algún símbolo b se tuviese que
si para algún símbolo b se tuviese que
![]() .
.
De manera recursiva, tenemos:
Utilizaremos un arreglo de sucesiones de cruce a revisar y otro de sucesiones de cruce ya revisadas.
 ,
,
Ejemplo
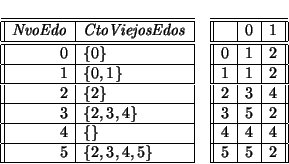
Para el autómata bidireccional
![]() ,
al aplicar el algoritmo anterior se distingue a las sucesiones de cruce
,
al aplicar el algoritmo anterior se distingue a las sucesiones de cruce
![\begin{displaymath}\begin{array}{\vert\vert r\vert l\vert\vert} \hline \hline
0...
...it Izq\/}), (0,\mbox{\it Der\/})]} \\ \hline \hline
\end{array}\end{displaymath}](img1159.gif)
Ejemplo
Para el autómata bidireccional
![]() ,
al aplicar el algoritmo anterior se distingue a 177 sucesiones de cruce para formar el autómata no-determinista AND. Cuando a éste se le convierte en uno determinista, digamos AD, aparecen 63 estados. El estado 0 de AND corresponde a la sucesión de cruce
,
al aplicar el algoritmo anterior se distingue a 177 sucesiones de cruce para formar el autómata no-determinista AND. Cuando a éste se le convierte en uno determinista, digamos AD, aparecen 63 estados. El estado 0 de AND corresponde a la sucesión de cruce
![]() .
El estado 0 de AD corresponde al conjunto de estados
.
El estado 0 de AD corresponde al conjunto de estados ![]() .
.
Vimos anteriormente que la palabra
 se lee por completo en el autómata
se lee por completo en el autómata
![]() y arriba a su estado 3. Cuando aplicamos
y arriba a su estado 3. Cuando aplicamos ![]() a AD se llega a su estado 49, el cual corresponde a la colección de estados de AND
a AD se llega a su estado 49, el cual corresponde a la colección de estados de AND