 definimos
definimos
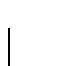 al conjunto de ``partes'' de
al conjunto de ``partes'' de
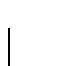 se cumplen las relaciones siguientes:
se cumplen las relaciones siguientes:
| K* | = | (15) | |
| = | (16) | ||
| = | (17) | ||
| (KL)*K | = | K(LK)* | (18) |
| (K+L)* | = | (K*L)*K* | (19) |
| (KL)* | = | (20) | |
| = | K* | (21) | |
| = | K* | (22) | |
| (K*)* | = | K* | (23) |
| = | (24) | ||
| K*K* | = | K* | (25) |
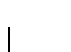 .
La ecuación (4.14) se sigue de las siguientes ecuaciones, justificadas ya anteriormente:
.
La ecuación (4.14) se sigue de las siguientes ecuaciones, justificadas ya anteriormente:
 .
Sea
.
Sea
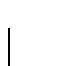 ,
y es tal que para cualesquiera dos lenguajes
,
y es tal que para cualesquiera dos lenguajes
 :
:
 (que de hecho coincide con la inclusión de conjuntos).
(que de hecho coincide con la inclusión de conjuntos).