the de Bruijn diagrams

Underlying the existence of the tiling is the fact that Rule 110 has semipermeable membranes. That is just a fancy way of saying that the sequence x10 always generates 1 (almost always - the ``semi'' comes from 111 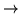$\rightarrow$ 0); more pertinent is that 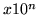$x10^n$ generates 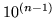$10^{(n-1)}$ which is another way of characterizing the triangles. Membranes are traceable to configurations in the de Bruijn diagram. It remains to be seen how directly this membrane affects the analysis of Rule 110, even though it is an integral part of the characterization of Rule 110 by tiling.

The reason for mentioning this is that it has been known that some rules have membranes bounding macrocells, within which evolution has to seek a cycle. But not all membranes are permanent, leading to the conjecture that their dissolution might be programmed. This is an idea which has probably never been followed up, but Rule 110 may actually be an instance which fits the pattern, since the evolution depends to a certain extent on the persistence of the left margin of the triangles, and the way in which it eventually breaks up.

In honor of the role of C gliders in Cook's introduction, the dimensions of the arrays in NXLCAU21 was raised to accomodate seven generations, with the result that they are described in a diagram of 556 nodes and 705 links. It is large for the multiplicity of ways the ether background can join to the T6's which in turn join to ether or vanish. To better manage the diagram, the self-node to the quiescent state can be excised, leaving a diagram of 502 nodes and 632 links; although only a 10% reduction, it takes away lots of stray lines from a map which is still extremely congested.

Table 1.2 summarizes the statistics on all the de Bruijn diagrams up to and including seven generations. The first row of each pair states the number of nodes, the second row, the number of links. When the two numbers coincide the diagram consists exclusively of loops, but not necessarily one single loop. Since zero is a quiescent state, entries of the form (1,1) indicate that it is the only configuration meeting the shifting requirement. In particular, there are no still lifes (except for zero).

The columns follow the degree of shifting, the remainder, pairs of rows, goes by generation.

Table 1.2: The number of nodes (upper number) and links (lower number) in the de Bruijn shift diagrams up to and including seven generations.

5 pt

-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7
85	46	26	15	9	5	1	1	1	5	10	19	34	60	106
85	46	26	15	9	5	1	1	1	5	10	19	34	60	106
42	31	22	19	10	1	1	9	1	9	15	5	33	24	90
42	31	22	19	10	1	1	11	1	9	15	5	33	24	90
75	23	38	19	1	5	9	19	1	27	22	37	42	5	134
75	23	38	19	1	5	9	22	1	35	22	37	42	5	134
42	68	26	13	1	41	15	17	1	1	10	13	26	47	109
42	68	26	13	1	49	15	19	1	1	10	13	26	47	109
110	19	1	23	10	58	1	86	9	116	42	38	66	14	161
110	19	1	23	10	63	1	102	9	142	42	38	66	14	161
85	31	94	99	1	27	100	57	1	15	1	126	26	48	85
85	31	100	111	1	27	112	62	1	15	1	164	26	48	85
14	219	9	129	1	266	1	556	1	5	18	1	69	5	169
14	239	9	136	1	287	1	705	1	5	18	1	69	5	169

Points of interest in the table, actually some of Cook's gliders, are the entries at (2,3) [A-gliders], at (-2.4) [B-gliders], and at (0,7) [C-gliders]. [The symbol (x,y) indicates a shift of x, negative to the left, in y generations].

Previously unreported gliders can be found at (2,5), (-1,6), and (-4,6). The (2,5) glider had already been observed in Cook's extensible gliders, but none of the three connects directly to Cook's ether.

Figure 1.19: Inventory of left shifting configurations. The quiescent configuration is an implicit component of every other shift; sometimes it is the only one. Otherwise it is not shown. When there are still more components, the panel is split into horizontal slices to accomodate them.

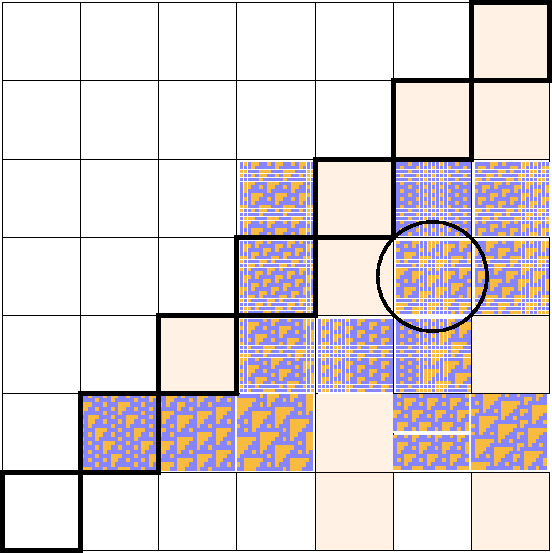Figure 1.20: Periodic configurations. The quiescent configuration is an implicit component of every other shift; sometimes it is the only one. Otherwise it is not shown. When there are still more components, the panel is split into horizontal slices to accomodate them. That is not the same as a one-sided ideal, in which one single panel divides into two distinctive regions along a vertical fissure.

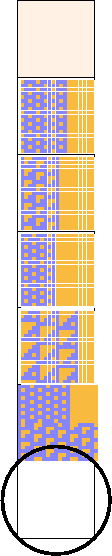Figure 1.21: Inventory of right shifting configurations. The horizontal coordinate determines the shift, the vertical coordinate the number of generations which have elapsed. The quiescent configuration is an implicit component of every other shift; sometimes it is the only one. Otherwise it is not shown.

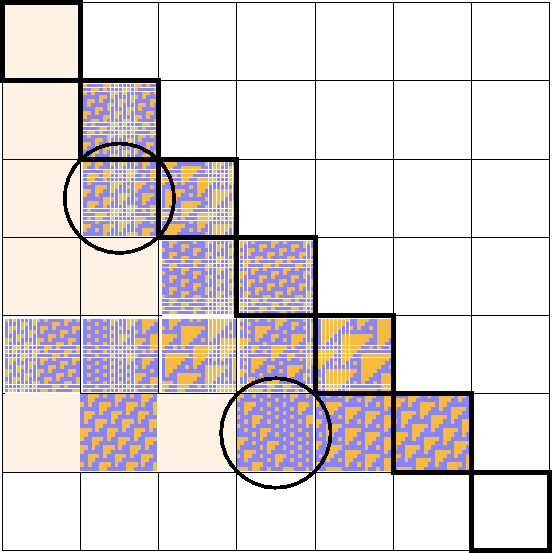Table 1.3: The number of nodes and links in the de Bruijn shift diagrams for eight generations.

5 pt

Shift	nodes	links	cycles	comments
---	---	---	------	-----
left 8	93	93	1, 4, 8, 90
left 7	56	56	1, 55
left 6	35	35	1, 34
left 5	182	193	2 components	Zero, and two big crosslinked cycles involving T7's. The interlinking makes for two packings, so a glider pairing could be imagined, as in some of the combinations seen previously.
left 4	381	447	doubled B's	The velocity is the same as for B gliders, with double the time available to complete the shift. The (-2)/4 B configuration must be a subset; it is an absorbing ideal paired with a T5 combination in an emitting ideal. This is a fuse, not gliders, and the figures move parallel to one another.
left 3	10	10	1, 9
left 2	37	37	1, 2x7, 22
left 1	38	38	1, 37
static	41	43	2 components	T1 emitting ideal connects to zero as an absorbing ideal in a diagram with 33 nodes, 35 links. An independent cycle length 8 contains a T2 mosaic.
right 1	22	22	1, 21
right 2	1	1	1
right 3	1	1	1
right 4	145	153	4 components	1) Quiescent zero configuration 2) T5's over T1's, in 2 phases 3) T1 emitting ideal connects to 4 different absorbing ideals, phases of T3's over T1's, which might be seen as some staggered B gliders.
right 5	208	208	1, 2x7, 193
right 6	152	152	various hashes
right 7	301	301	several	a variety of cycles, some of them rather pretty.
right 8	13	13	1, 4, 8

Table 1.4: The number of nodes and links in the de Bruijn left shift diagrams for nine generations.

5 pt

Shift	nodes	links	cycles	comments
---	---	---	------	-----
left 9	10	10	1, 9	Zero, T2's stacked vertically
left 8	57	57	1, 4x14	This combination is important because it is one of the two in the ninth generation in which the crystallography of the ether tiles allows gliders. We see the zero configuration and four of spatial period (cycle) 14, of which one is the ether lattice and the other three phases of a salvo of fat A gliders with seven T1's, even though they conform to a left-moving displacement criterion. Since only the one combination is allowed and there are no alternatives, this mixture might not be a glider even though it has the appearance of one.
left 7	1	1	1	only the quiescent configuration
left 6	59	59	1, 3x12, 3x6, 4
left 5	26	26	1, 25
left 4	216	225	fuse	4-high A's defer to diagonally stacked T8's.
left 3	9	9	1, 8
left 2	370	406	1, fuse	Zero, and a component in which T1's form the emitting ideal, a combination of T8, T3, and 3 T1's repeat to constitute the absorbing ideal.
left 1	587	666	1, mixed	A combination of T8, T3, and two T1's remimiscent of the C glider; they can waver in their vertical alignment in a way which could be construed as forming a glider family.

Table 1.5: The number of nodes and links in the de Bruijn static and right shift diagrams for nine generations.

5 pt

Shift	nodes	links	cycles	comments
---	---	---	------	-----
static	689	771	big diagram	Includes the T2 emitter, Zero absorber visible in the third generation as one component, There is also a glider bombardment of a T5 wall, and the T5 wall as a source of B glider salvos which annihilate an oncoming A salvo. This is a ``black hole'' configuration which often forms from two oppositely directed shift configurations. The T5's form an absorbing ideal which contains one of the two allotropic forms of the gliders previously found in the ``four left in six generations'' analysis.
right 1	1	1	1
right 2	5	5	1, 4
right 3	1	1	1
right 4	1	1	1
right 5	34	34	1, 8, 25
right 6	604	784	1, A's	Zero, all kinds of A's but nothing evident which was not already visible with the ``2 left every 3'' row, so there are neither double nor triple A-bar's. This is the other shift combination for which the ether lattice could have had ninth generation gliders.
right 7	125	125	1, 124
right 8	51	51	1, 50
right 9	94	94	1, 9, 21, 63