two right in five generations

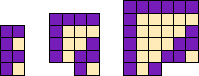
Amongst the gliders so far discovered, there seems to be a preference for leftward motion, with only A and D gliders running to the right. However, an additional one, which might be called an alpha glideralpha glider, was discovered among the de Bruijn diagrams. Once their discovery was made, they were found to be an essential element in the formation of Cook's extensible E and G gliders; others seem to have been aware of their existence, such as their mention by Li and Nordahl [4].

**Figure 2.1:** There are three species of composite tile from which gliders of velocity 2/5 c arise.
$\begin{figure}\centering\begin{picture}(140,50) \put(0,-10){\epsfxsize = 140pt \epsffile{t2in5a.eps}} \end{picture}\end{figure}$

If the T1's are used, they extend inexorably to the left. On the other hand, the other two can be mixed at will, so that either can be a glider against a background formed by the other. As a philosophical point in glider theory, it should be recognized that a structure is best regarded as a glider when it stands out against a background, thereby supposing a thin glider with fat background.

**Figure 2.2:** Reading left to right, the T1 tiles can be repeated until they meet a T3, following which T3's and T5's may repeat or alternate arbitrarily.
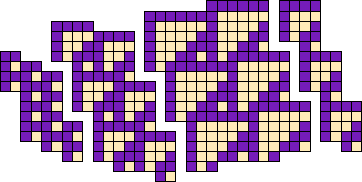$\begin{figure}\centering\begin{picture}(240,120) \put(0,0){\epsfxsize = 240pt \epsffile{t2in5b.eps}} \end{picture}\end{figure}$

The T3's aren't ether tiles because the T1 is always stuck on to them. But they can readily join up with other T3's, especially in the form of glider collisions. However, the relative positioning of the T1 appendage differs between B gliders and E gliders. In the same spirit, a crosscurrent of B gliders can be seen in a thick layer of the second speciesspecies, running between source and sink T5's.

Once the de Bruijn diagram for a shift-generation combination is available, the relationships between the different structures visible in the field of evolution is greatly clarified. Of course, it can turn out that the de Bruijn diagram iteslf defies comprehension, as the number of vertices and links increases with the number of generations.

Figure 2.3 shows the de Bruijn diagram for the $\alpha$ gliders. To begin with, the vertex of ten zeroes is self-linked and isolated from all other vertices. That is the quiescent configuration, which would have any shifting characteristic immaginable. If it is isolated, then any other pattern must extend to infinity, but if there are interconnections, there may be regions of activity separated by quiescent regions, or there may be quiescent half-spaces. ``Islands of chaos in seas of tranquility'' was Wolfram's poetic description of Class IV behavior.

**Figure 2.3:** The de Bruijn diagram provides the only satisfactory description of the interrelation between the three $\alpha$ species. The cycles of length 10 are the five phases of where T5's and T3's alternate. However there are also domains of pure T1-T5 ``squares'' and domains of pure B gliders.
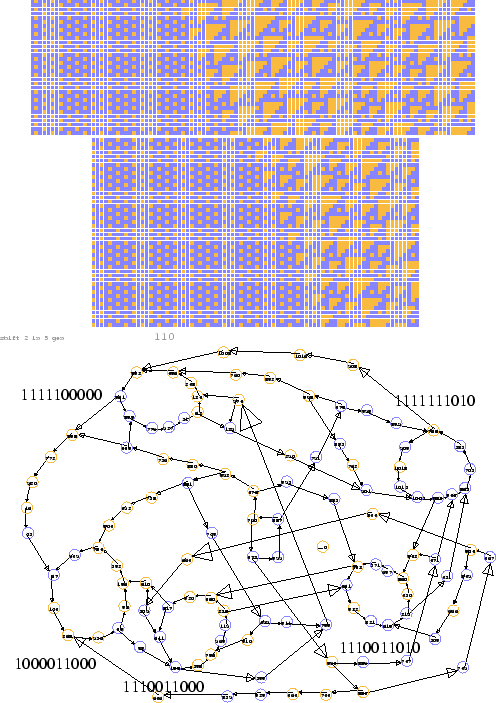$\begin{figure}\centering\begin{picture}(340,420) \put(0,0){\epsfxsize = 340pt \epsffile{db2in5.eps}} \end{picture}\end{figure}$

Zero need not be the only absorbing component or emitting component, as the loop of length 4 in this diagram shows. As an emitting component, it defines left-hand behavior which, once discontinued, can never resume. The strict loop generates the T1 tiling, the first of the three species of gliders. There are five loops of length ten. If any one of them is followed out, it will be seen to comprise a slice through one T3, one T5, and a T1 nestled between them. It is no one single species, but a mixture having cycle ten and period five; however that turns out to be one of the primitive loops - loops of shortest length in virtue of having no shorter subloop.

**Figure 2.4:** Detail of the interface between a sublattice of alpha glider symmetry and the ether lattice. Notice how the location of the marginal T1's should be adjusted to ensure continuity along the interface..
$\begin{figure}\centering\begin{picture}(200,280) \put(0,-10){\epsfxsize = 200pt \epsffile{alfethiface.eps}} \end{picture}\end{figure}$

The five loops are not really independent, since they correspond to the five different phases of evolution followed by a cyclic repetition of any one of them. Of course the number of loops could be a divisor of the period of the diagram; but since 5 is prime that could be only 1 or 5, but 1 would mean the strict shift of a sequence unchanging from generation to generation.

One lesson to be learned is that there is not necessarily a strict correspondence between prime loops in the de Bruijn diagram and species of glider.

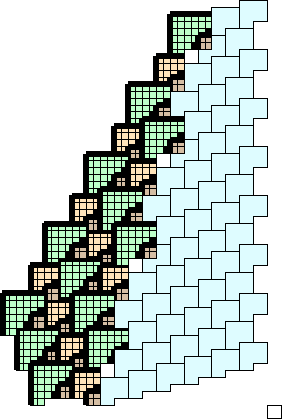
A detail concerning the alpha lattice which is important for the construction of gliders, but which will not show up until one examined the shift symmetry left four in fifteen generations, is the fact that there are sublattices compatible with the ether lattice.