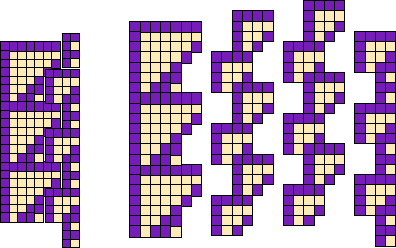The C gliders are based on T6 tiles, which must be supplemented if they are to fill up the plane. Placing a T1 just under the diagonal at bottom left creates a niche for a T3 just to its right, but which is better kept separate.
Thus the first tile is the combined T1 and T6, which has a height of seven cells. The second tile has two T3's, one above and slightly to the right of the other, for a combined height of eight cells. But this pair can be stacked in a vertical column by aligning the top row of the bottom tile with the bottom row of the lower tile, once again an effective height of seven.
Another combination with a height of seven and stackable in a vertical column compatible with either of the first two tiles, is the third tile shown at the far right in Figure 2.22. It is built from a stack of two T1's nestled under a T3, whose staggered four-three left margin is congruent to the margin in the T3 stack.
The T6ish tiles have a left margin which is a vertical spine - a column of 1's which extends indefinitely, which is just the left margin of a whimsical T
. Meanwhile the third tile, featuring T1's, has a similar right margin. As a result, T6's which have been connected to none or more T3's can reconnect to another T6 to create an environment in which T6's and T3's alternate; or they can connect to a zero half-space, from which there is no return. In other words, a static fuse can exist.
Figure 2.23 summarizes the sequences which can be formed, all of period 7. The columnar form of some of the margins is to be noted; it is related to the ability to interface with a half-space of zeroes, and on a more modest scale, with any large triangle..
