 |
The one dimensional binary cellular automaton rule numbered 110 in Stephen Wolfram's system of identification [9] has been an object of especial attention because of glider-like structures which have been observed in samples of evolution from random initial conditions. It has even been suggested that it belongs to that exceptional Class IV of automata whose chaotic aspects are intermingled with regularities of behavior; it is just that the background against which this development occurrs is textured rather than quiescent, a tacit assumption in the original classification.
Whatever the merits of the classification, Rule 110 was awarded its own appendix (Table 15) in reference [9], containing specimens of evolution annotated with a list of thirteen gliders compiled by Doug Lind and the conjecture that the rule might be ``universal.''
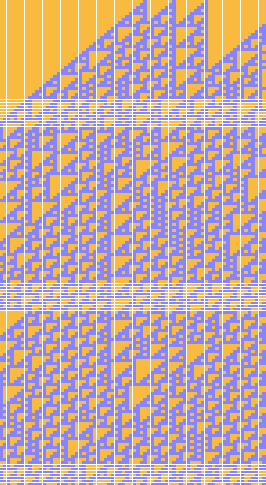
Figure 1.1 contains a similar evolutionary sample, starting out from a sparse collection of ones; the scale of diagrams such as these affects the ease with which gliders are perceived. Complementarity applies; the more visible the glider tracks, the harder to grasp the finer details of their structure.
There does not seem to be much published literature concentrating on Rule 110; the sole exception seems to be some statistical studies [4] done by Wentian Li and Mats Nordahl around 1992. The transitional role of Rule 110, as relates to its Class IV style positioning between Wolfram's Classes II and III, would seem to be reflected in a slow approach to equilibrium statistics, via a power law rather than exponentially.
As for information available via Internet, Matthew Cook wrote an eight page introduction [1] listing gliders A through H and a glider gun. Cook cites Erik Winfree as having made an exhaustive enumeration of Rule 110 gliders, and cross links to Winfree's www page, which, however, does not seem to mention this particular feat. Another brief page [10] exists in the Santa Fe Institute ALife archive.
Looking at the rule itself, there seems to be a ubiquitous background texture which Cook calls ``ether'' although it is but one of many regular lattices stable under the rule's evolution, and not the one with the smallest unit cell. Calling the artifacts which turn up ``gliders'' is a way of speaking, no doubt borrowed from experience based on Life. Alternatively, they might be termed ``dislocations'' and studied as lattice defects.
Taking that approach is suggested by observing that the basic entities in the lattices, the unit cells, are hollow upside down isosceles right triangles of varying sizes. The significance of using Rule 110 colud be in guaranteeing recognizably distinct tiles to be assembled, and now that we know that the rule is supposed to be ``universal'' we might look towards the evolution as a tiling problem, in the sense of Hao Wang. It might even be possible to see fitting elements of one lattice into another as an instance of Post's correspondence principle, which would establish the computational complexity of the evolution right off.
The choice of words such as ``gliders'' or ``dislocations'' is really quite subjective. The name glider originates from John Conway's Life, to describe small five-cell mobile artifacts relative to the quiescent background of a two-dimensional cellular automaton. It is a mixture of a technical term from crystallography, alluding to a four stage cycle in which mirror images of the phases particpate; and a certain whimsey suggesting a gracefullnes of motion. It has came to mean anything that moves; moreover in the case of Rule 110, against a background which is no longer quiescent, but textured.
Further complicating the analysis, and suggesting the appropriateness of at least an occasional reference to defects and dislocations, is the fact that two or more distinguishable patterns alternate with one another, or rotate in sequence. When one pattern is highly dominant and the others a rarity, the unusual constituents can be perceived visually as gliders. But roles can be reversed. Even worse, they can occur in approximately equal numbers haphazardly mixed, at which point talking about a disordered, or partially ordered, lattice may be more appropriate than picking out gliders.
In Life, fuses are related to gliders except for extending to infinity. Similar structures abound in Rule 110, where they are readily regarded as the junction of two dissimilar lattices whose interface shifts with time.