next up previous contents
Next: C - EBar collisions Up: Collisions with C gliders Previous: C - D collisions   Contents

C - E collisions

Any description of collisions with E gliders can become quite complicated simply because of the large variety of E gliders once their extensibility has been reckoned with. From a much larger perspective, there is far less variation because large E gliders are really margins of the alpha lattice, whose interface with other lattices is periodic on a sufficiently large scale.

Figure 3.29: Some selected collisions amongst C, E, EBar, and F gliders exhibit the properties of solitons.
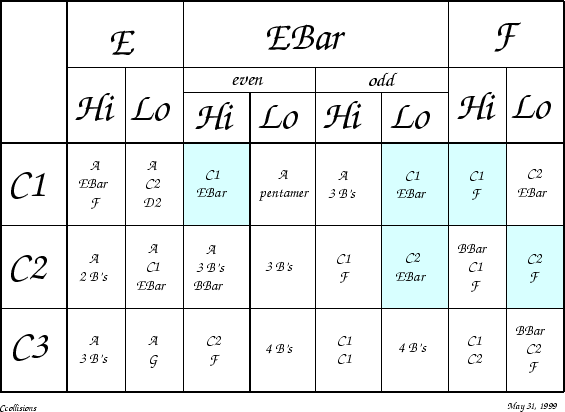\begin{figure}\centering\begin{picture}(372,300) \put(0,0){\epsfxsize = 372pt \epsffile{clls.eps}} \end{picture}\end{figure}

Figure 3.30: A pair of C's standing to the left can act as an En decrementer similar to an A coming in from the left. Still others simply get eaten away as the En dissolves into a burst of B gliders which the next C in line refurbishes into another En.
\begin{figure}\centering\begin{picture}(320,420) \put(0,0){\epsfxsize = 320pt \epsffile{CEN.eps}} \end{picture}\end{figure}

Figure 3.31: Many collisions with E complexes simply unravel the margin of an 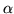$\alpha$ domain, which means that they will always follow a predictable pattern.
\begin{figure}\centering\begin{picture}(360,420) \put(0,0){\epsfxsize = 360pt \epsffile{margin.eps}} \end{picture}\end{figure}

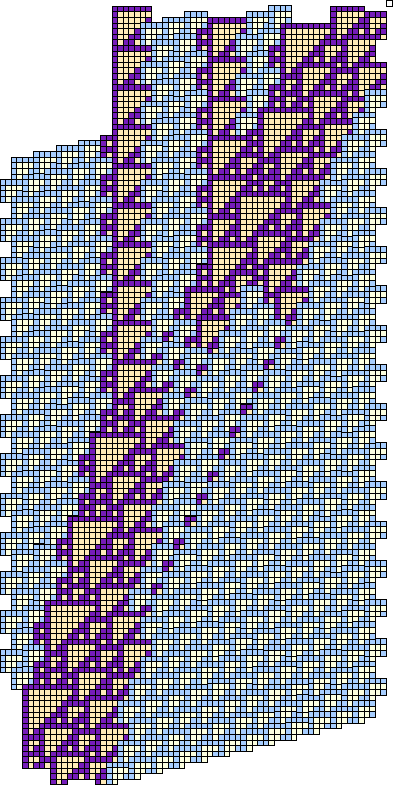
Figure 3.32: C2 collides with E, producing a shower of B's. These can collide with a waiting C2 to restore the E, but with decremented index.
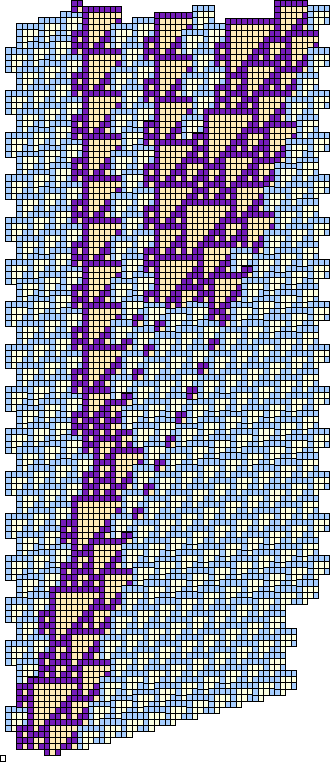\begin{figure}\centering\begin{picture}(220,450) \put(0,0){\epsfxsize = 220pt \epsffile{edown.eps}} \end{picture}\end{figure}

Figure 3.33: En eats up C3's, fattening itself in the process.
\begin{figure}\centering\begin{picture}(250,480) \put(0,0){\epsfxsize = 250pt \epsffile{C3C3.eps}} \end{picture}\end{figure}

next up previous contents
Next: C - EBar collisions Up: Collisions with C gliders Previous: C - D collisions   Contents
Jose Manuel Gomez Soto 2002-01-31