Running an Obstacle Course

Having enumerated binary collisions and examined some of their products, attention naturally turns to more complicated collisions. If the reactants are well separated, it is just a matter of combining the binary results. But given that collisions take time to resolve themselves, a third (or even more) gliders can intrude into the reaction area, changing the final result.

An intermediate type of collision consists of those where the interaction is perfectly predictable, but the combination of a whole series may turn out to be interesting. One example lies in the use of an En as a counter, which can be manipulated by two different mechanisms.

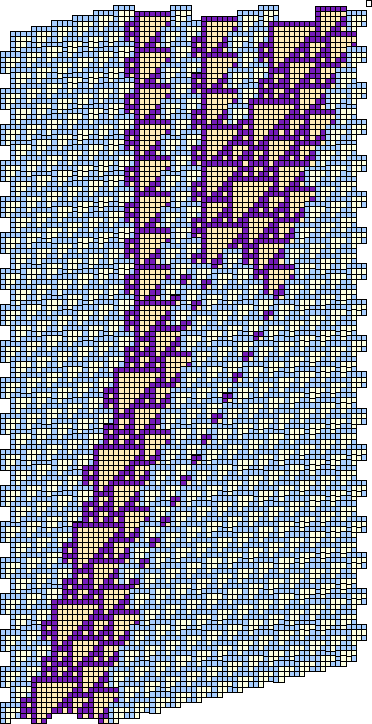
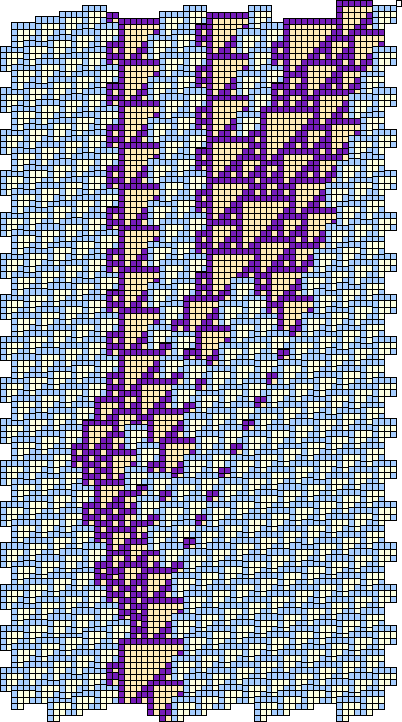
The outstanding characteristic of an En glider is that $n$ will be incremented by B collisions, surely and independently of their relative spacing. Two of the possible collisions by an A glider decrement the index (taking $E_0$ as D1, and observing that B D1 can bring the E back, thereby allowing a mild deficit). Although symmetrical with respect to the indices, the arrival of the index modifying gliders from opposite directions reccommends isolating the En, complicating any plans to use it as a tally.

The other index changing collision arrangement uses C gliders (which, of course, are static), relying upon the difference between C2 or C3 to get the sign of the index change. Whichever, the modifier sits on the same side, always the left, of the oncoming E. Creating a series of index changes depends on arranging the sign changing C's in the required linear order.

Running off the end of the series, with a non-existent $E_0$, also has to be foreseen and provided for.

Figure 4.1: Left: A pair of C2's can decrement an En. Right: A pair of C3's can increment an En.

Figure 4.2: By alternating incrementation and decrementation, an En can maintain itself while erasing (right to left) C2, C3 pairs. Incrementing, followed by decrementing, is secure; reversing the order could create an EBar as an intermediate.

Figure 4.3: Unfortunately, reversing the order of C2 and C3 in an En sweep breaks the sequence, introducing EBars. The T10 visible at the bottom of the figure is a canonical EBar precursor.

Figure 4.4: The C3 - E collision creates a B triad plus an A. But an A - E collision, high or low, produces a C3. Therefore a C3 can move to the right against an E stream at the expense of releasing three B gliders for every two E's which it absorbs. All those B's could be used to produce a huge E at some point, if that were desired.

Figure 4.5: A slowly drifting complex can be formed from an infinite sequence of A, C2, and D2 gliders. Absorption of the A during the triple collision leads to regeneration of the C - D pair and the emission of a new A. The A's can be used to link successive pairs to get a figure with an overall shift period of 2 left every 86 generations.